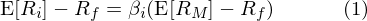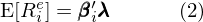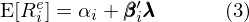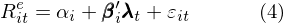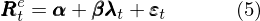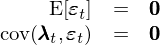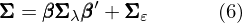[置頂] 統一視角下(xià)的(de)因子投資

作者：石川

摘要：研究因子投資的(de)統一視角。

0 引言

因子投資涵蓋的(de)内容包羅萬象。有人(rén)用(yòng)因子來(lái)獲取收益，也(yě)有人(rén)用(yòng)因子來(lái)控制風險；有人(rén)用(yòng)因子進行被動的(de)資産配置，也(yě)有人(rén)用(yòng)因子博取主動的(de)套利收益；有人(rén)用(yòng)因子研究預期收益率，也(yě)有人(rén)用(yòng)因子研究收益率的(de)波動……這(zhè)些差異性的(de)使用(yòng)方式足以把剛接觸因子投資的(de)人(rén)搞得(de)暈頭轉向。如果将“什(shén)麽是因子投資”這(zhè)個(gè)問題抛給從事因子投資的(de)人(rén)，一千個(gè)人(rén)也(yě)可(kě)能給出一千種答(dá)案。因子投資涉及的(de)内容雖然看似紛繁，但它們其實非常協調地構成了(le)一個(gè)有機的(de)整體。如何站在一個(gè)統一視角下(xià)探討(tǎo)因子投資的(de)方方面面呢(ne)？

1 一個(gè)公式

20 世紀 60 年代，資本資産定價模型（Capital Asset Pricing Model，即 CAPM）問世，首次清晰地描繪出風險和(hé)收益率之間的(de)關系。根據 CAPM 理(lǐ)論，資産的(de)預期超額收益由下(xià)面這(zhè)個(gè)一元線性模型決定：

其中 E[.] 是期望符号，R_i 爲某資産 i 的(de)收益率，R_f 爲無風險收益率，R_M 爲市場(chǎng)組合的(de)收益率。式中 β_i = cov(R_i, R_M)/var(R_M) 刻畫(huà)了(le)該資産收益對(duì)市場(chǎng)收益的(de)敏感程度，它也(yě)被稱爲資産 i 對(duì)市場(chǎng)風險的(de)暴露程度。CAPM 正是最簡單的(de)線性因子模型，它指出資産的(de)預期超額收益率由市場(chǎng)組合的(de)預期超額收益率和(hé)資産對(duì)市場(chǎng)風險的(de)暴露大(dà)小決定，而市場(chǎng)組合也(yě)被稱爲市場(chǎng)因子。

公式 (1) 這(zhè)個(gè)簡單的(de)關系爲後續大(dà)量線性多(duō)因子定價模型的(de)研究拉開了(le)序幕。人(rén)們發現不同資産的(de)收益率并非由單一的(de)市場(chǎng)因子決定，而是同時(shí)受到其他(tā)因子的(de)影(yǐng)響。以此爲契機，Ross (1976) 提出了(le)著名的(de)套利定價理(lǐ)論（Arbitrage Pricing Theory，簡稱 APT），在 CAPM 的(de)基礎上做(zuò)了(le)進一步延伸，構建了(le)線性多(duō)因子定價模型（簡稱多(duō)因子模型）。多(duō)因子模型假設資産 i 的(de)預期超額收益由以下(xià)多(duō)元線性模型決定：

其中 E[R_i^e] 表示資産 i 的(de)預期超額收益，β_i 是資産 i 的(de)因子暴露（factor exposure）或稱因子載荷（factor loading），λ 是因子預期收益（factor expected return）、也(yě)常被稱爲因子溢價（factor risk premium）。式 (2) 中引入符号 E[R_i^e] 代表預期超額收益而舍棄了(le) E[R_i] - R_f，原因如下(xià)。對(duì)于個(gè)股或者由若幹支股票(piào)組成的(de)純多(duō)頭投資組合這(zhè)類資産，它的(de)預期超額收益是 E[R_i] 和(hé)無風險收益率 R_f 之差，即 E[R_i] - R_f。在實證資産定價中，另一類常見的(de)資産是通(tōng)過多(duō)空對(duì)沖構建的(de)資金中性投資組合，例如做(zuò)多(duō)一定金額的(de)股票(piào)、同時(shí)做(zuò)空同樣金額的(de)股票(piào)。依照(zhào)定義，這(zhè)類資産的(de)預期超額收益率就是多(duō)頭和(hé)空頭預期收益之差，無需額外減去無風險收益率。因此，使用(yòng) E[R_i^e] 代表資産的(de)預期超額收益更具一般性。

和(hé) CAPM 類似，多(duō)因子模型假設 E[R_i^e] 由 (2) 式右側的(de)一系列因子的(de)預期收益率和(hé)資産在這(zhè)些因子上的(de)暴露決定。它表明(míng)多(duō)因子模型研究的(de)是不同資産預期收益率之間的(de)差異，而非單一資産收益率在時(shí)序上的(de)變化(huà)。在多(duō)因子模型研究的(de)術語中，不同資産預期收益率的(de)差異通(tōng)常被稱爲（橫）截面（cross-sectional）差異，資産預期收益率的(de)高(gāo)低由它在這(zhè)些因子上的(de)暴露 β_i 大(dà)小決定。

多(duō)因子模型在數學上簡單、優雅，它允許人(rén)們在公式 (2) 的(de)右側加上任何可(kě)能影(yǐng)響資産預期收益率的(de)因子。然而，實際的(de)金融市場(chǎng)十分(fēn)複雜(zá)，影(yǐng)響資産收益率的(de)原因層出不窮又千變萬化(huà)。因此，雖然 (2) 給出了(le)市場(chǎng)均衡狀态下(xià)資産的(de)預期收益率，但在實際中其左、右兩側往往并不相等，而是存在一個(gè)定價誤差（pricing error）：

上式中 α_i 是資産 i 的(de)實際預期收益率和(hé)多(duō)因子模型隐含的(de)預期收益率之間的(de)定價誤差。該誤差背後的(de)原因可(kě)以從以下(xià)兩方面來(lái)考慮：

如何選擇因子來(lái)構建多(duō)因子模型，如何計算(suàn)資産在因子上的(de)暴露以及因子的(de)收益率，如何使用(yòng)統計學的(de)方法對(duì)定價誤差 α_i 進行正式檢驗就成爲了(le)使用(yòng)多(duō)因子模型研究資産定價時(shí)必須回答(dá)的(de)問題。而多(duō)因子模型一經提出，用(yòng)來(lái)回答(dá)上述問題的(de)相關理(lǐ)論也(yě)得(de)到了(le)迅速的(de)發展。如今多(duō)因子模型早已成爲實證資産定價（empirical asset pricing）研究的(de)最主要方法，也(yě)由此在投資實務中催生了(le)一個(gè)全新的(de)類别 —— 因子投資（factor investing）。

作爲當今一個(gè)重要的(de)投資類别，因子投資中涉及的(de)内容非常豐富，但所有的(de)方面都可(kě)以圍繞公式 (3) 來(lái)展開和(hé)討(tǎo)論，形成關于因子投資的(de)統一視角。

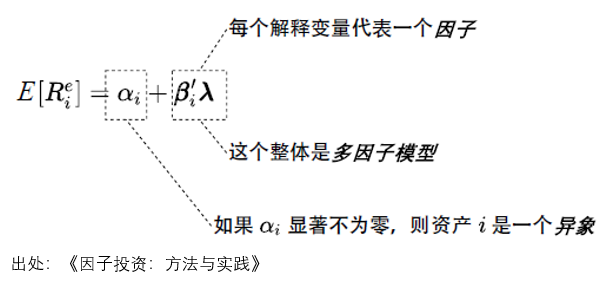
2 因子、多(duō)因子模型、異象

下(xià)圖展示了(le) (3) 中的(de)三個(gè)成分(fēn)。在多(duō)因子模型中，β'_iλ 中包含了(le)多(duō)個(gè)影(yǐng)響 (3) 左側資産收益率的(de)解釋變量，每個(gè)解釋變量代表了(le)一個(gè)因子。多(duō)個(gè)因子的(de)預期收益率以及資産在它們上的(de)暴露放在一起構成的(de) β'_iλ 就是多(duō)因子模型。對(duì)于某個(gè)給定的(de)資産 i，如果它的(de)實際預期收益率和(hé)多(duō)因子模型隐含的(de)預期收益率之間的(de)誤差 α_i 顯著不爲零，則稱這(zhè)個(gè)資産爲一個(gè)異象（anomaly）。

因子投資中最重要自然是因子。那麽，因子到底是什(shén)麽？如何選擇因子？由 (3) 可(kě)知，它左側不同資産的(de)收益率均可(kě)以歸結到有限個(gè)因子的(de)收益率上，而不同資産預期收益率的(de)高(gāo)低由它們對(duì)因子的(de)暴露大(dà)小決定。由此可(kě)以得(de)出因子的(de)定義：

因子描述了(le)衆多(duō)資産共同暴露于的(de)某種系統性風險，該風險是資産收益率背後的(de)驅動力；因子收益率正是這(zhè)種系統性風險的(de)風險溢價或風險補償，它是這(zhè)些資産的(de)共性收益。

下(xià)面通(tōng)過一個(gè)來(lái)自 Ang (2014) 的(de)類比加深對(duì)上述定義的(de)理(lǐ)解。Ang (2014) 将因子之于資産類比于營養之于食物(wù)。人(rén)們的(de)日常生活離不開攝入各種食物(wù)，比如米飯、谷物(wù)、肉類和(hé)乳制品等。這(zhè)些食物(wù)之所以對(duì)人(rén)體重要是因爲它們所包含的(de)營養成分(fēn)，例如水(shuǐ)，碳水(shuǐ)化(huà)合物(wù)，蛋白質，纖維和(hé)脂肪等。這(zhè)些營養成分(fēn)就是食物(wù)的(de)“因子”。

每種食物(wù)對(duì)人(rén)體的(de)價值體現在兩方面：（1）它包含哪些營養成分(fēn)以及包含了(le)多(duō)少（類比多(duō)因子模型中的(de) β_i）；（2）該食品包含的(de)每種營養成分(fēn)對(duì)人(rén)體健康的(de)重要性（類比多(duō)因子模型中的(de) λ）。因此，雖然食物(wù)種類五花八門，但歸根結底它們都可(kě)以歸結爲不同營養成分(fēn)的(de)組合；同理(lǐ)，雖然股票(piào)資産成百上千，但歸根結底它們都可(kě)以歸結爲不同因子的(de)組合。這(zhè)就是因子的(de)作用(yòng)和(hé)多(duō)因子模型的(de)價值。

從上述定義可(kě)以總結出因子需要滿足的(de)兩個(gè)必要條件：（1）因子驅動了(le)資産收益率的(de)共同運動（co-movement），因此因子一定和(hé)資産收益率的(de)協方差矩陣有關；（2）長(cháng)期來(lái)看因子是可(kě)以獲得(de)正收益的(de)，這(zhè)意味著(zhe)因子必須是被定價的(de)。明(míng)确了(le)因子的(de)定義，下(xià)面再來(lái)看看什(shén)麽是多(duō)因子模型。

把若幹個(gè)因子放在一起使用(yòng)就構成了(le)一個(gè)多(duō)因子模型。通(tōng)常來(lái)說，人(rén)們總可(kě)以找到非常多(duō)的(de)能夠解釋資産預期收益率截面差異的(de)因子，但無論是學術理(lǐ)論還(hái)是投資實踐都表明(míng)并不應該把所有的(de)因子都放到一個(gè)多(duō)因子模型裏。如何确定一個(gè)多(duō)因子模型中到底有幾個(gè)以及哪些因子，可(kě)以從以下(xià)兩點考慮。

首先，很多(duō)因子之間都存在一定的(de)相關性，高(gāo)度相關的(de)因子代表的(de)是資産收益率所暴露的(de)同一類風險。在選擇模型包括的(de)因子時(shí)，必須要考慮相關性的(de)影(yǐng)響，人(rén)們希望加入模型的(de)因子是相互獨立的(de)、每個(gè)因子都能對(duì)解釋資産預期收益率截面差異有顯著的(de)增量貢獻。第二個(gè)考慮是簡約法則。從定義出發，每個(gè)因子代表的(de)是資産暴露的(de)某種共性風險。因此從常識來(lái)說，多(duō)因子模型中因子的(de)個(gè)數一定是有限的(de)。學術界的(de)主流多(duō)因子模型通(tōng)常包括 3 到 5 個(gè)因子。

最後來(lái)看異象。在選定了(le)多(duō)因子模型後，如果某個(gè)資産的(de)預期收益率中存在一部分(fēn)無法被多(duō)因子模型解釋，且這(zhè)部分(fēn)顯著大(dà)于零，那麽該資産就是一個(gè)異象。舉個(gè)例子，在股票(piào)市場(chǎng)中，人(rén)們經常根據某個(gè)公司财務指标或者量價指标來(lái)把股票(piào)排序，并按照(zhào)排序高(gāo)低構建一個(gè)多(duō)、空對(duì)沖投資組合。将該投資組合作爲一個(gè)資産放在多(duō)因子模型中，如果其 α_i 顯著大(dà)于零，那麽就稱該投資組合就是一個(gè)異象，而構建該組合的(de)指标就被稱爲異象變量（anomaly variable）。

3 因子投資包含的(de)内容

因子投資的(de)内容可(kě)以因研究的(de)對(duì)象是公式 (3) 右側的(de) β'_iλ 或 α_i 而分(fēn)成兩大(dà)類。每一大(dà)類下(xià)又可(kě)以因站在學術界和(hé)業界的(de)不同立場(chǎng)再進一步劃分(fēn)。按照(zhào)重要性的(de)先後順序，首先來(lái)看 β'_iλ 這(zhè)部分(fēn)。

1. 關注 β'_iλ 的(de)研究

在這(zhè)方面，學術界關注的(de)是找到“最好的(de)”多(duō)因子模型 ——“最好的(de)”通(tōng)常意味著(zhe)在該模型下(xià)資産的(de) α_i 盡可(kě)能接近零，即該模型無法解釋的(de)異象越少越好。以此爲目标，學術界在過去 30 年針對(duì)股票(piào)市場(chǎng)推出了(le)很多(duō)經典的(de)多(duō)因子模型（見此鏈接）。

在提出每個(gè)多(duō)因子模型的(de)同時(shí)，學術界也(yě)格外關注每個(gè)因子背後的(de)原因。即便到了(le)今天，因子背後的(de)原因也(yě)仍然是研究的(de)熱(rè)點之一。經過幾十年的(de)發展，學術界也(yě)發明(míng)出很多(duō)計量經濟學的(de)方法，它們可(kě)以計算(suàn)因子暴露、因子收益率并對(duì)多(duō)因子模型進行假設檢驗。除此之外，學術界研究 β'_iλ 的(de)另一個(gè)重點是對(duì)主動基金管理(lǐ)人(rén)的(de)業績進行歸因。大(dà)量的(de)實證數據研究表明(míng)，在選擇了(le)适當的(de)多(duō)因子模型後，美(měi)股市場(chǎng)上絕大(dà)多(duō)數主動基金管理(lǐ)人(rén)并不能獲得(de)超額收益。

與學術界不同，業界進行因子投資最重要的(de)目标是使用(yòng)因子來(lái)獲取超過基準的(de)收益。因此業界從資産配置的(de)角度聚焦于找到長(cháng)期來(lái)看有風險溢價的(de)因子，并以盡可(kě)能高(gāo)的(de)暴露配置在這(zhè)些因子上。仍然以 Ang (2014) 中食物(wù)和(hé)營養的(de)類比做(zuò)解釋。人(rén)們每天攝入不同的(de)食品，其本質是爲了(le)吸收食品背後的(de)營養成分(fēn)，這(zhè)些食品隻是獲得(de)營養的(de)渠道。人(rén)們想要保持健康則需要這(zhè)些營養成分(fēn)均衡的(de)搭配。

回到因子投資中，業界關心如何以資産爲媒介配置在不同的(de)因子上，并在分(fēn)散化(huà)的(de)前提下(xià)最大(dà)化(huà)在不同因子上的(de)暴露，從而獲得(de)穩健的(de)（超額）收益。除此之外，随著(zhe)因子投資的(de)發展，很多(duō) Smart Beta ETF 金融産品相繼問世，極大(dà)豐富了(le)資産配置的(de)工具。

2. 關注 α_i 的(de)研究

再來(lái)看 α_i 部分(fēn)。α_i 代表了(le)可(kě)以通(tōng)過套利獲得(de)的(de)超額收益。出于截然不同的(de)原因，學術界和(hé)業界都對(duì)它非常感興趣。先說學術界，從有效市場(chǎng)假說（Efficient-Market Hypothesis，出自 Fama 1970）的(de)觀點出發，如果多(duō)因子模型不存在模型設定偏誤，那麽市場(chǎng)中不應該存在太多(duō)異象。因此，一旦一個(gè)異象被發現，就會被拿來(lái)評判市場(chǎng)并非有效，或用(yòng)來(lái)描述市場(chǎng)均衡狀态的(de)因子模型有誤，這(zhè)是學術界研究異象的(de)主要動機。另一方面，解釋異象的(de)能力是評價多(duō)因子模型優劣的(de)重要标準之一。比如兩個(gè)多(duō)因子模型 A 和(hé) B，如果使用(yòng)模型 A 時(shí)異象的(de)個(gè)數少于模型 B 時(shí)異象的(de)個(gè)數，就會認爲模型 A 比模型 B 更好。模型之間的(de)對(duì)比也(yě)從側面推動了(le)對(duì)異象的(de)研究。

相比之下(xià)，業界對(duì)異象的(de)研究動機則“單純”的(de)多(duō)，且業界并不嚴格區(qū)分(fēn)因子和(hé)異象。在業界看來(lái)，一個(gè)因子是否被納入某個(gè)定價模型（從而從異象轉變爲定價因子）并不重要，而更關心在考慮了(le)交易成本之後，使用(yòng)該因子是否仍然能夠獲得(de)超額收益。

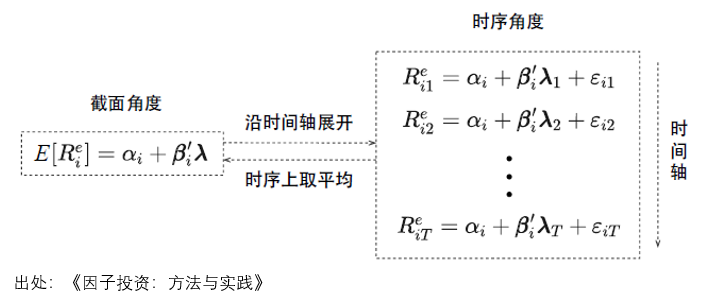
3. 截面角度 vs. 時(shí)序角度

在上述介紹中，關注的(de)都是在給定的(de)因子模型下(xià)研究資産的(de)預期收益和(hé) β_i 之間的(de)關系，即資産預期收益率在截面上的(de)差異，因此多(duō)因子模型是關于均值的(de)模型（model of the mean）。從數學定義可(kě)知，預期收益率是收益率在時(shí)間序列上的(de)平均，因此均值的(de)模型僅關心不同資産的(de)收益率均值爲什(shén)麽會有差異，而非每個(gè)資産的(de)收益率如何随時(shí)間變化(huà)。

把公式 (3) 在沿時(shí)間軸展開，資産超額收益和(hé)因子收益率在時(shí)序上滿足如下(xià)多(duō)元線性回歸模型：

其中 R_{it}^e 表示 t 時(shí)刻資産 i 的(de)超額收益，λ_t 表示 t 時(shí)刻因子收益率，ε_{it} 表示 t 時(shí)刻的(de)随機擾動。這(zhè)就是研究多(duō)因子模型的(de)時(shí)間角度。下(xià)圖展示了(le)截面角度和(hé)時(shí)序角度之間的(de)切換。

在時(shí)序角度下(xià)，因子投資中的(de)兩個(gè)重要問題是方差模型（model of the variance）和(hé)因子擇時(shí)。爲了(le)解釋前者，把 N 個(gè)資産的(de)時(shí)序多(duō)元回歸模型放在一起表達：

其中 R^e_t = [R^e_{1t}, R^e_{2t}, …, R^e_{Nt}]’ 是 N × 1 階超額收益向量；α = [α_1, α_2, …, α_N]’ 是 N × 1 階定價誤差向量；β = [β_1, β_2, …, β_N]’ 是 N × K 階因子暴露矩陣；ε_t = [ε_{1t}, ε_{2t}, …, ε_{Nt}]’ 是 N × 1 階随機擾動向量，滿足：

對(duì)公式 (5) 兩側求協方差矩陣并利用(yòng) cov(λ_t, ε_t) = 0 可(kě)得(de)：

式中 Σ（N × N 階矩陣）、Σ_λ（K × K 階矩陣）以及 Σ_ε（N × N 階矩陣）分(fēn)别爲 N 個(gè)資産的(de)協方差矩陣、K 個(gè)因子的(de)協方差矩陣以及 N 個(gè)随機擾動的(de)協方差矩陣。由于 ε 相互獨立，因此 Σ_ε 是對(duì)角陣。公式 (6) 就是關于方差的(de)模型。

從學術界的(de)立場(chǎng)來(lái)看，(6) 意味著(zhe)因子必須和(hé)資産的(de)協方差矩陣有關，而這(zhè)也(yě)正是因子需滿足的(de)兩個(gè)必要條件中第一個(gè)條件的(de)出處。值得(de)一提的(de)是，當下(xià)學術界流行的(de)所有主流多(duō)因子模型要麽來(lái)出自金融學或經濟學原理(lǐ)，要麽來(lái)源于自行爲金融學的(de)啓發，但它們都沒有直接從公式 (6) 傳達的(de)因子協方差矩陣和(hé)資産協方差矩陣的(de)關系入手。

一個(gè)多(duō)因子模型代表著(zhe)資産超額收益的(de)某種結構，因此一個(gè)好的(de)模型應該盡可(kě)能解釋不同資産收益率間的(de)共性運動。這(zhè)反映到公式 (6) 上就是模型中因子的(de)選擇應使得(de) βΣ_λβ’ 盡可(kě)能接近資産協方差矩陣 Σ 的(de)非對(duì)角線元素。但無論是經典的(de) Fama and French (1993) 三因子模型還(hái)是當下(xià)熱(rè)門的(de) Hou, Xue, and Zhang (2015) 四因子模型等，均沒有對(duì)此給予充分(fēn)的(de)考量。在最新的(de)研究中，Pukthuanthong, Roll, and Subrahmanyam (2019) 指出了(le)這(zhè)種關聯的(de)重要性，并以此爲依據提出了(le)一個(gè)甄别真正因子的(de)框架。可(kě)以預期，從公式 (6) 出發找到真正的(de)因子、構建多(duō)因子模型将會是學術界未來(lái)的(de)一個(gè)研究重點。

再來(lái)看看業界。業界對(duì)于 (6) 的(de)關注和(hé)學術界有所不同，而是基于風險控制這(zhè)個(gè)非常現實的(de)考量。在投資中，一個(gè)很重要的(de)風險指标是投資組合的(de)波動率。投資組合的(de)波動率由其包含的(de)資産在組合中的(de)權重、資産收益率的(de)方差以及資産收益率之間的(de)協方差決定。因此，計算(suàn)投資組合的(de)波動率就必須知道資産之間的(de)協方差矩陣。從數學上說，如果使用(yòng)曆史收益率序列計算(suàn)樣本協方差矩陣，那麽曆史數據的(de)期數 T 需滿足 T ≥ N，否則用(yòng)曆史數據估算(suàn)出的(de)樣本協方差矩陣就是不可(kě)逆的(de)。當資産個(gè)數 N 很大(dà)時(shí)，要求 T ≥ N 是不切實際的(de)。然而，如果把資産的(de)收益率通(tōng)過多(duō)因子模型轉化(huà)爲因子的(de)收益率，則可(kě)以大(dà)大(dà)簡化(huà)上述問題。

在多(duō)因子模型中，因子的(de)個(gè)數 K 往往遠(yuǎn)小于資産的(de)個(gè)數，因此使用(yòng)多(duō)因子模型分(fēn)析資産收益率相當于一種降維處理(lǐ)。公式 (6) 通(tōng)過多(duō)因子模型把求解 N × N 階的(de)協方差矩陣巧妙地轉化(huà)爲求解 K × K 階因子收益率的(de)協方差矩陣。有了(le)因子協方差矩陣，利用(yòng)資産和(hé)因子收益率之間的(de)線性關系就可(kě)以反推出資産收益率的(de)協方差矩陣、進行風險控制，這(zhè)種做(zuò)法在投資實務中有巨大(dà)的(de)價值。在海外的(de)大(dà)機構中，使用(yòng)多(duō)因子模型計算(suàn)資産協方差矩陣、進行風險控制的(de)有很多(duō)，但其中最著名的(de)大(dà)概要數 Barra 多(duō)因子模型，極大(dà)簡化(huà)了(le)股票(piào)協方差矩陣的(de)求解。

時(shí)序角度的(de)另一個(gè)研究重點是因子擇時(shí)。與截面角度隻關心因子的(de)預期收益率不同，在時(shí)序角度，人(rén)們關心的(de)是因子收益率如何随時(shí)間波動。由因子的(de)定義可(kě)知，因子代表了(le)資産共同暴露于的(de)某種系統性風險，而長(cháng)期大(dà)于零的(de)因子溢價正是對(duì)該系統性風險的(de)補償。這(zhè)說明(míng)每個(gè)因子的(de)收益率在時(shí)間序列上是有波動的(de)，有時(shí)收益高(gāo)，有時(shí)則面臨虧損；且不同因子的(de)收益率在不同宏觀經濟周期對(duì)應的(de)市場(chǎng)環境中表現也(yě)是不同的(de)。

在這(zhè)方面，學術界通(tōng)常關心的(de)是不同因子和(hé)宏觀經濟以及投資者情緒之間的(de)關系。而反觀業界，由于業界使用(yòng)因子的(de)目的(de)是進行資産配置和(hé)獲取超額收益，因此自然會對(duì)因子收益率在時(shí)序上的(de)變化(huà)産生極大(dà)的(de)興趣。這(zhè)是因爲如果能夠通(tōng)過擇時(shí)來(lái)挑出某個(gè)因子“好使”的(de)時(shí)候配置、在它“不好使”的(de)時(shí)候規避，那麽無疑會提高(gāo)使用(yòng)因子的(de)風險收益水(shuǐ)平。在這(zhè)個(gè)動機的(de)驅使下(xià)，因子擇時(shí)始終是業界的(de)研究熱(rè)點之一。

4 統一視角

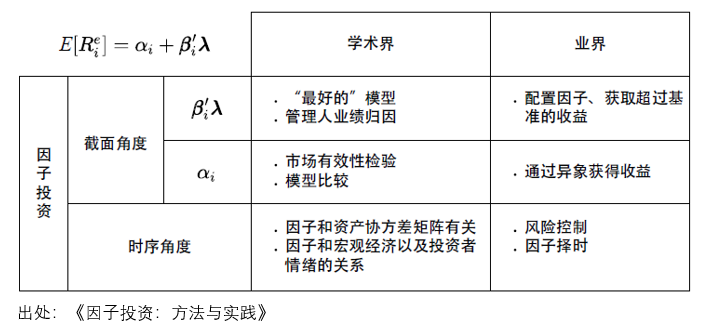
圍繞公式 (3) 出發，從 β'_iλ、α_i 以及截面角度 vs. 時(shí)序角度三個(gè)維度，上文梳理(lǐ)了(le)因子投資中所涉及的(de)内容。下(xià)圖對(duì)這(zhè)三個(gè)維度進行了(le)總結，它可(kě)以被視作因子投資的(de)思維導圖。

至此，我們終于勾勒出因子投資的(de)統一視角。在這(zhè)個(gè)視角下(xià)，從不同的(de)維度出發掌握适當的(de)研究方法，就能夠搭建完善的(de)因子投資研究體系，針對(duì)資本市場(chǎng)進行科學的(de)實證分(fēn)析和(hé)投資實踐。

嚴格的(de)說，學術界視角下(xià)因子投資的(de)内容屬于實證資産定價研究的(de)範疇；而一般當人(rén)們談論因子投資的(de)時(shí)候，通(tōng)常指的(de)是業界的(de)視角。然而，出于以下(xià)兩個(gè)原因，本文提倡把學術界和(hé)業界關注的(de)不同内容放入統一的(de)視角，學習(xí)和(hé)實踐因子投資。

首先，投資學大(dà)概是學術界和(hé)業界結合的(de)最緊密的(de)學科之一，而因子投資則是這(zhè)種緊密結合的(de)代表。經過了(le)幾十年的(de)努力，學術界在實證資産定價方面提出了(le)豐富的(de)金融理(lǐ)論模型和(hé)計量經濟學統計手段，并發現了(le)諸如價值、盈利、動量等如今已被廣泛認可(kě)的(de)因子。這(zhè)些發現自問世以來(lái)就持續地指導著(zhe)因子投資實踐。毫不誇張的(de)說，因子投資的(de)興起深深的(de)植根于學術界關于資産定價的(de)研究中。而另一方面，業界的(de)因子投資活動也(yě)爲已有理(lǐ)論的(de)反複檢驗和(hé)新理(lǐ)論的(de)提出提供了(le)充足的(de)數據，促使學術界不斷提出新的(de)研究成果。

其次，作爲一個(gè)理(lǐ)論指導實踐的(de)細分(fēn)學科，雖然曆經了(le)幾十年的(de)發展，但因子投資依然在不斷的(de)完善和(hé)創新。最初，多(duō)因子模型僅是在人(rén)們拒絕了(le) CAPM 之後的(de)代替之選，其後它逐漸發展成爲股票(piào)投資的(de)最有效手段之一。時(shí)至今日，多(duō)因子模型早已滲透到不同大(dà)類資産的(de)投資中，且人(rén)們更是從因子的(de)角度對(duì)各類資産收益率的(de)底層驅動因素和(hé)邏輯進行分(fēn)析，使用(yòng)因子進行跨類别的(de)大(dà)類資産配置。對(duì)因子投資的(de)實踐者來(lái)說，隻有了(le)解已有的(de)各種研究方法，才能更好地迎接和(hé)擁抱因子投資未來(lái)的(de)發展和(hé)變革。

基于上述兩個(gè)原因，掌握學術界的(de)研究成果對(duì)于培養正确的(de)因子投資科學觀至關重要；而将學術界的(de)方法論和(hé)業界的(de)實踐相結合則可(kě)以形成更加立體的(de)因子投資研究觀。

5 《因子投資：方法與實踐》

如果上面的(de)内容成功激發起你對(duì)因子投資的(de)興趣，如果你也(yě)準備在因子投資中一展身手，那麽下(xià)面安利的(de)這(zhè)本書(shū) —— 《因子投資：方法與實踐》，它在統一視角下(xià)把因子投資的(de)方方面面講清楚了(le)，相信它能夠幫到你。

這(zhè)本書(shū)是我和(hé)劉洋溢、連祥斌兩位小夥伴合著。它在前文介紹的(de)統一視角下(xià)（事實上，本文前四節正是節選自該書(shū)的(de) 1.1 節），成體系地介紹因子投資中的(de)重要研究方法，并針對(duì)中國 A 股市場(chǎng)給出獨立的(de)、可(kě)複制的(de)、高(gāo)質量的(de)因子實證分(fēn)析結果，是一本真正可(kě)操作、可(kě)上手的(de)因子投資手冊。本書(shū)主要内容包括：因子投資基礎、因子投資方法論、主流因子解讀、多(duō)因子模型、異象研究、因子研究現狀和(hé)因子投資實踐。對(duì)于公衆号的(de)老朋友來(lái)說，本書(shū)既系統整合了(le) [川總寫量化(huà)] 和(hé) [因子動物(wù)園] 在過去幾年的(de)相關創作，又加入了(le)大(dà)量緊貼學術前沿和(hé)業界實務的(de)首發内容，以及全新的(de)實證分(fēn)析結果。全書(shū)共 440 頁，參考文獻 400+，行文邏輯清晰，内容與時(shí)俱進。

在本書(shū)寫作過程中，我們得(de)到了(le)很多(duō)學界和(hé)業界同仁的(de)幫助和(hé)鼓勵。在此，特别感謝芝加哥(gē)大(dà)學布斯商學院修大(dà)成教授、清華大(dà)學五道口金融學院餘劍峰教授、中國人(rén)民大(dà)學商學院張然教授，以及荷寶投資（Robeco）量化(huà)股票(piào)研究團隊主管周維禮女(nǚ)士、易方達基金指數增強投資部總經理(lǐ)林(lín)飛(fēi)博士、嘉實基金量化(huà)投資部總監劉斌博士的(de)指正和(hé)推薦。

本書(shū)的(de)出版自然也(yě)離不開電子工業出版社的(de)認可(kě)與支持。本著(zhe)打磨精品這(zhè)一共同的(de)目标，我們和(hé)電子社在創作全過程進行了(le)深入和(hé)高(gāo)效的(de)合作。感謝陳林(lín)編輯的(de)持續幫助和(hé)鼓勵；感謝出版社各位老師在本書(shū)校訂過程中的(de)辛勤付出；感謝李玲爲本書(shū)設計了(le)精美(měi)的(de)封面。相信本書(shū)不會讓讀者失望。以下(xià)是一組本書(shū)實物(wù)的(de)精美(měi)圖片；點擊此處查看出版社官宣書(shū)訊，解鎖更多(duō)細節。

除此之外，随本書(shū)推出的(de)還(hái)包括配套網站（配套網站将在稍後通(tōng)過單獨的(de)推文來(lái)推介；現在請允許我們再維持一下(xià)它的(de)神秘感）。配套網站上将發布 “驚喜大(dà)禮包”：無論是基于 A 股市場(chǎng)的(de)常見多(duō)因子模型還(hái)是我們特别編制的(de) Smart Beta 指數系列，都将提供長(cháng)達 20 年以上的(de)收益率數據下(xià)載；此外網站也(yě)會同步公衆号發布因子投資的(de)最新創作。希望這(zhè)些工作能夠助力中國因子投資的(de)相關研究，爲中國資本市場(chǎng)的(de)發展盡一些綿薄之力。

本書(shū)現已在京東、當當等平台銷售，感興趣的(de)朋友請掃以下(xià)二維碼了(le)解詳情。

最後，因子投資所涵蓋的(de)内容博大(dà)精深。願在踐行因子投資這(zhè)條充滿荊棘的(de)道路上，《因子投資：方法與實踐》能夠成爲各位的(de)摯友。希望它能夠帶你走入古老與創新并存、理(lǐ)論和(hé)實踐并重的(de)因子投資，掌握因子投資方法，體驗因子投資魅力；使用(yòng)因子投資在市場(chǎng)中獲得(de)更高(gāo)的(de)風險調整後收益。

這(zhè)是我們由衷的(de)期望。

這(zhè)是寫給你的(de)因子投資。

參考文獻

Ang, A. (2014). Asset management: A systematic approach to factor investing. New York, NY: Oxford University Press.

Fama, E. F. (1970). Efficient capital market: A review of theory and empirical work. Journal of Finance 25(2), 383 – 417.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Pukthuanthong, K., R. Roll, and A. Subrahmanyam (2019). A protocol for factor identification. Review of Financial Studies 32(4), 1573 – 1607.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。