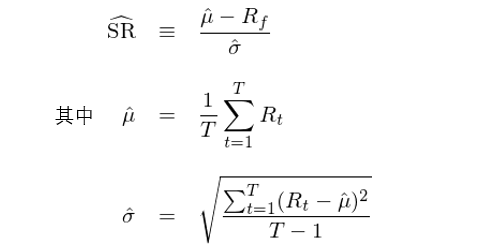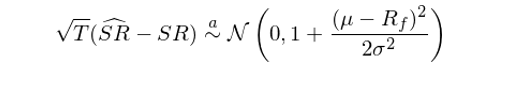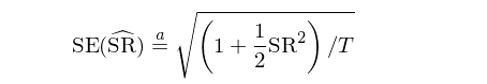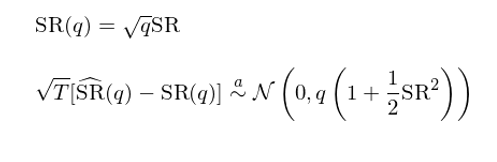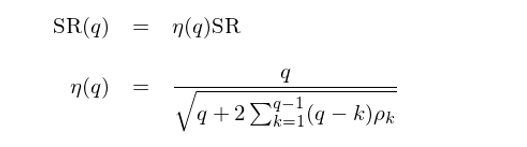夏普比率随想

作者：石川

摘要：人(rén)人(rén)都熟知夏普比率，但隻有當它被使用(yòng)得(de)當時(shí)，才能提高(gāo)投資管理(lǐ)水(shuǐ)平。

1 夏普比率

在投資領域，夏普比率（Sharpe Ratio）是人(rén)們耳熟能詳的(de)一個(gè)概念。它因爲同時(shí)考慮了(le)回報和(hé)風險而成爲衡量一個(gè)策略，或者基金業績的(de)核心指标之一。最初在 William Sharpe 提出這(zhè)個(gè)概念的(de)時(shí)候（Sharpe 1966），它的(de)名字叫 Reward-to-Variability Ratio (R/V)，這(zhè)個(gè)名字很好的(de)反映了(le)它的(de)實質；不過後來(lái)，這(zhè)個(gè)名字被人(rén)們談及的(de)越來(lái)越少，人(rén)們更願意使用(yòng)“夏普比率”這(zhè)個(gè)叫法。

在 William Sharpe 自己解讀夏普比率的(de)一篇文章(zhāng)（Sharpe 1994）中，它指出夏普比率分(fēn)爲事前夏普比率（the Ex Ante Sharpe Ratio）以及事後夏普比率（the Ex Post Sharpe Ratio）。前者使用(yòng)對(duì)未來(lái)單期收益率均值和(hé)标準差的(de)預測進行計算(suàn)，而後者使用(yòng)曆史數據計算(suàn)。通(tōng)常，當我們談及夏普比率的(de)時(shí)候，默認的(de)都是後者。

按照(zhào) Sharpe (1994) 的(de)定義，假設 R_t 爲 t 期的(de)收益率，R_f 爲無風險收益率，則使用(yòng) t = 1 到 T 這(zhè)段長(cháng)度的(de)曆史數據計算(suàn)的(de)（事後）夏普比率爲：

用(yòng)白話(huà)說，如果标準差可(kě)以理(lǐ)解爲風險的(de)代理(lǐ)指标後，那麽夏普比率度量的(de)就是風險調整後的(de)超額收益。在上面的(de)公式中，無論是夏普比率、收益率均值還(hái)是标準差，它們的(de)符号上面都有一個(gè)上标，說明(míng)它們是從樣本數據中估計出來(lái)的(de)數據。它是否能準确的(de)衡量過去一段時(shí)間一個(gè)策略或一支基金的(de)真實夏普比率呢(ne)？本文的(de)第三節會回答(dá)這(zhè)個(gè)問題。

今天我們就來(lái)聊聊夏普比率。文章(zhāng)每節都會圍繞著(zhe)夏普比率這(zhè)個(gè)概念，但每節獨立自成一個(gè)方面。因此我稱它爲“夏普比率随想”。希望讀完能帶給你一點點啓發，重新審視這(zhè)個(gè)“我們自認爲理(lǐ)解的(de)不能不能的(de)了(le)”的(de)夏普比率。

2 直觀上認識

談到夏普比率，首先要說明(míng)計算(suàn)它的(de)頻(pín)率。人(rén)們通(tōng)常所說的(de)夏普比率是年化(huà)夏普比率。那麽，對(duì)于一個(gè)量化(huà)投資策略，年化(huà)夏普比率多(duō)大(dà)才比較好的(de)？一般來(lái)說，如果一個(gè)策略在回測中的(de)年化(huà)夏普比率（扣除各種交易成本後）小于 1，它就沒有什(shén)麽繼續被研究的(de)價值了(le)（确實殘酷）。很多(duō)量化(huà)對(duì)沖基金往往要求回測中的(de)年化(huà)夏普比率超過 2；更有甚者（某家全球上著名的(de)量化(huà)對(duì)沖基金）僅僅考慮年化(huà)夏普比率大(dà)于 3 的(de)策略。

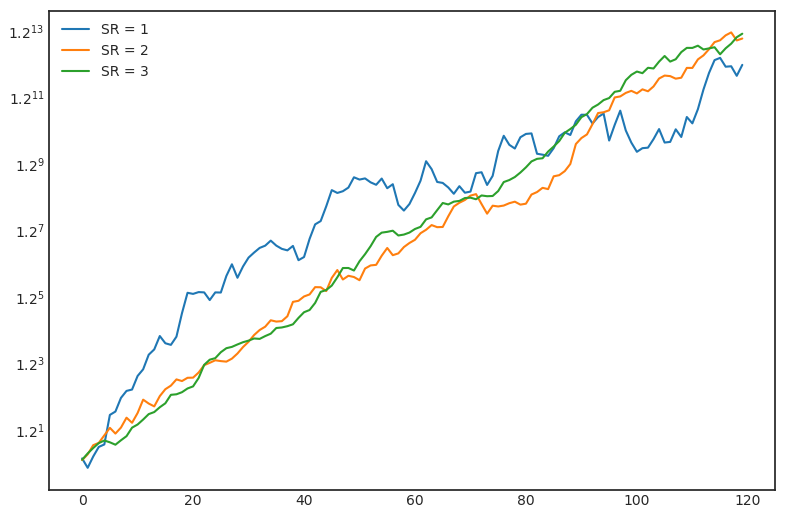
年化(huà)夏普比率爲 1、2 甚至是 3 是什(shén)麽概念呢(ne)？下(xià)圖是假象的(de)三條淨值曲線。它們都是假設投資長(cháng)度爲十年，并使用(yòng)正态分(fēn)布随機生成的(de)月(yuè)頻(pín)收益率（均值爲 2%），然後按照(zhào)給定的(de)年化(huà)夏普比率反推出收益率的(de)标準差。

當年化(huà)夏普比率爲 3 時(shí)，淨值曲線（在縱軸爲對(duì)數坐(zuò)标時(shí)）基本上是一條直線了(le)；當年化(huà)夏普比率爲 2 時(shí)，它的(de)淨值曲線也(yě)僅在局部有一些小的(de)波動；當年化(huà)夏普比率爲 1 時(shí)，它的(de)淨值曲線在全局範圍内呈現出更大(dà)的(de)波動；即便如此它也(yě)是個(gè)靠譜的(de)賺錢策略（想想 A 股各大(dà)指數長(cháng)期以來(lái)可(kě)憐的(de)夏普比率）。

上面的(de)例子告訴我們，當（年化(huà)）夏普比率爲 3 的(de)時(shí)候，淨值曲線基本上就是一直漲，可(kě)想而知其難度。但是我們往往在市場(chǎng)上能看到一些策略，它們計算(suàn)出來(lái)的(de)（年化(huà)）夏普比率往往比 3 還(hái)高(gāo)，有些還(hái)高(gāo)的(de)離譜。這(zhè)個(gè)現象背後的(de)一種解釋是，頻(pín)率越高(gāo)的(de)策略，夏普比率可(kě)能越高(gāo)；特别是對(duì)于那些高(gāo)頻(pín)策略，幾乎每天賺錢的(de)那種，兩位數的(de)夏普比率都絕非罕見。

我絕不否認市場(chǎng)中有這(zhè)種“神一般的(de)存在”，但是超高(gāo)夏普比率的(de)背後恐怕還(hái)有一個(gè)更合理(lǐ)的(de)解釋 —— 年化(huà)的(de)時(shí)候計算(suàn)錯了(le)，過度的(de)高(gāo)估了(le)年化(huà)夏普比率。爲了(le)說明(míng)這(zhè)一點，下(xià)面就來(lái)看看夏普比率的(de)統計特性。

3 統計特性

在本文第 1 節介紹（事後）夏普比率的(de)公式中，夏普比率（包括計算(suàn)它的(de)收益率均值和(hé)标準差）是從樣本數據中估計出來(lái)的(de)數據；它僅僅是某個(gè)策略或者基金業績在過去一段時(shí)間内真實（但未知）的(de)夏普比率的(de)一個(gè)估計。它最緻命的(de)問題是沒有考慮單期收益率之間的(de)相關性（下(xià)面英文是 Sharpe 1994 中談及夏普比率計算(suàn)公式中沒有考慮相關性的(de)部分(fēn)），這(zhè)将造成樣本夏普比率和(hé)真實夏普比率之間的(de)誤差。更重要的(de)是，在使用(yòng)高(gāo)頻(pín)夏普比率來(lái)推導年化(huà)夏普比率的(de)時(shí)候，不考慮單期收益率的(de)相關性将造成年化(huà)夏普比率估計的(de)巨大(dà)誤差。

爲了(le)定量分(fēn)析樣本夏普比率和(hé)真實夏普比率之間的(de)誤差，以及從高(gāo)頻(pín)（比如日頻(pín)、周頻(pín)、月(yuè)頻(pín)）夏普比率推算(suàn)低頻(pín)（比如年化(huà)）夏普比率時(shí)的(de)誤差，Lo (2002) 研究了(le)夏普比率的(de)統計性質。對(duì)于最簡單的(de)情況 —— 假設單期收益率滿足 IID 分(fēn)布，則樣本夏普比率對(duì)真實夏普比率估計的(de)漸近分(fēn)布滿足：

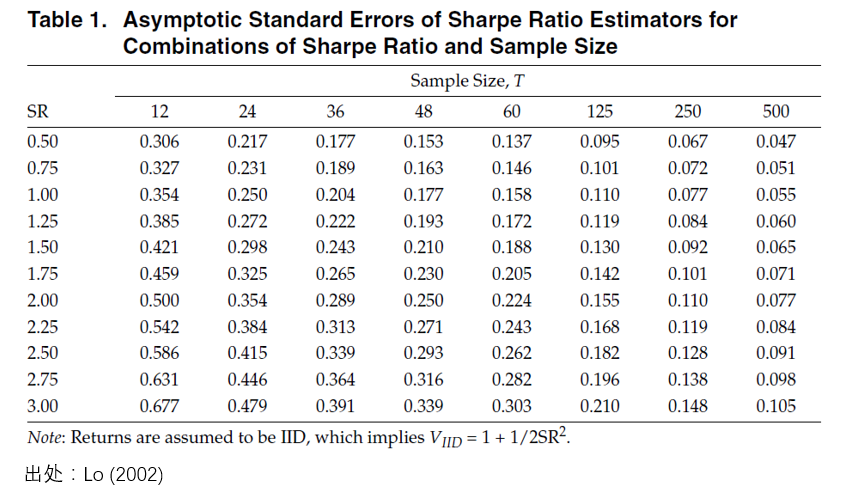
其中 μ、σ 和(hé) SR 分(fēn)别表示單期收益率的(de)真實均值、标準差和(hé)以它們計算(suàn)出的(de)真實夏普比率。由此可(kě)知，樣本夏普比率的(de) Standard Error 滿足：

在實際使用(yòng)時(shí)，可(kě)以在上式中将真實夏普比率替換爲樣本夏普比率。下(xià)圖給出了(le)不同夏普比率和(hé)樣本個(gè)數對(duì)應的(de)夏普比率估計誤差（Lo 2002）。夏普比率越高(gāo)，它的(de) standard error 越大(dà)；而當樣本個(gè)數小的(de)時(shí)候，這(zhè)個(gè)問題更加嚴重。所以，如果有人(rén)隻給你看了(le)很短的(de)業績，并告訴你一個(gè)很高(gāo)的(de)夏普比率，那就要小心了(le)。

如果單期收益率不滿足 IID 分(fēn)布，則估算(suàn)樣本夏普比率的(de)誤差更複雜(zá)一些，但仍可(kě)以使用(yòng) GMM 方法求解，具體參見 Lo (2002)。再來(lái)看看用(yòng)高(gāo)頻(pín)夏普比率推算(suàn)低頻(pín)夏普比率的(de)情況。假如我們有使用(yòng)月(yuè)頻(pín)收益率計算(suàn)出的(de)夏普比率，當把它換算(suàn)成年化(huà)夏普比率的(de)時(shí)候，常見的(de)做(zuò)法是乘以根号 12。然而，這(zhè)種做(zuò)法正确的(de)前提是，單期（這(zhè)裏是月(yuè)頻(pín)）收益率滿足 IID。一旦這(zhè)個(gè)假設不成立，上述計算(suàn)方法就有不小的(de)問題。

首先仍然考慮最簡單的(de) IID 情況。令 SR(q) 表示 q 期真實夏普比率，Lo (2002) 給出如下(xià)結果：

下(xià)面來(lái)考慮非 IID 的(de)情況，即單期收益率之間存在自相關性（可(kě)能是正的(de)，也(yě)可(kě)能是負的(de)）。假設收益率滿足平穩性、令 ρ_k 表示間隔 k 期的(de)自相關系數，則有：

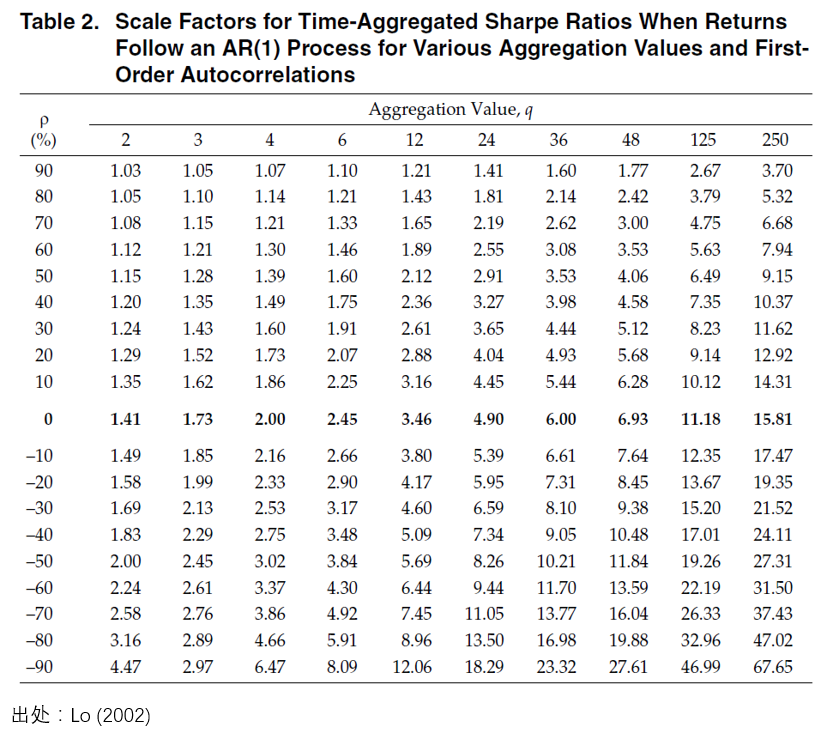
可(kě)見，當單期收益率之間不滿足 IID 時(shí)，計算(suàn) q 期夏普比率就不能簡單的(de)乘以根号 q 了(le)，而是要計算(suàn)一個(gè)系數 η(q)，它和(hé)收益率的(de)各階自相關系數有關。對(duì)于最簡單的(de) AR(1) 情況，η(q) 和(hé)期數 q 以及自相關系數 ρ 的(de)關系可(kě)以從下(xià)面這(zhè)個(gè)表中感受一二。

表中 ρ = 0 對(duì)應的(de)是根号 q。當 ρ > 0 時(shí)（收益率正相關），η(q) 小于根号 q；說明(míng)當收益率正相關時(shí)，按照(zhào)傳統方法計算(suàn)的(de) q 期夏普比率高(gāo)估了(le)其真實值。當 ρ < 0 時(shí)（收益率負相關），η(q) 大(dà)于根号 q；說明(míng)當收益率負相關時(shí)，按照(zhào)傳統方法計算(suàn)的(de) q 期夏普比率低估了(le)其真實值。

這(zhè)樣的(de)結果不難理(lǐ)解。當計算(suàn) q 期夏普比率的(de)時(shí)候，對(duì)于 IID 的(de)情況，收益率按 q 增長(cháng)，而标準差随根号 q 增長(cháng)，因此最終夏普比率按照(zhào) q/sqrt(q) = 根号 q 增長(cháng)。但是當收益率之間有正（負）相關時(shí)，标準差的(de)增長(cháng)要快(kuài)（慢(màn)）于 IID 的(de)情況，導緻 η(q) 大(dà)（小）于根号 q。

總結一下(xià)，本節的(de)介紹說明(míng)以下(xià)兩點：

最後，對(duì)于那些想要進一步研究 Lo (2002) 成果的(de)小夥伴，需要指出的(de)是他(tā)在研究 q 期夏普比率的(de)統計特性時(shí)，使用(yòng)的(de)是單期的(de)百分(fēn)比收益率而非對(duì)數收益率，因此結果是一種近似。Lin and Chou (2003) 指出當投資期限很長(cháng)時(shí)，不考慮複利的(de)影(yǐng)響也(yě)會在計算(suàn)夏普比率時(shí)産生誤差。

4 夏普比率檢驗策略是否有效

最後來(lái)聊聊随想的(de)最後一個(gè)部分(fēn)。有效市場(chǎng)假說拉開了(le)學術界和(hé)業界關于市場(chǎng)有效性長(cháng)達數十年的(de)探討(tǎo)。如果将“有效性”這(zhè)個(gè)概念放在一個(gè)策略上又如何呢(ne)？

我經常在券商報告上看到這(zhè)樣的(de)論調：首先通(tōng)過一個(gè)目标算(suàn)法找到了(le)一個(gè)策略 A，回測中得(de)到了(le)不錯的(de)效果；然後又在 A 的(de)基礎上加上了(le)某種 ensemble 算(suàn)法得(de)到了(le)策略 B，并指出這(zhè)個(gè)策略 B 取得(de)了(le)比 A 更加優異的(de)風險收益比（即夏普比率）。

這(zhè)個(gè)結果說明(míng)策略 B 比策略 A 更加有效。換句話(huà)說，如果一個(gè)策略可(kě)以通(tōng)過進一步的(de)擇時(shí)或者其他(tā)直接作用(yòng)于該策略收益率序列的(de)任何算(suàn)法，使得(de)它的(de)夏普比率進一步提高(gāo)，那麽這(zhè)個(gè)策略就不是有效的(de)。基于此提出以下(xià)猜想：一個(gè)有效的(de)策略應該是時(shí)序收益率均值爲正，且每期收益率之間滿足 IID 分(fēn)布，它的(de)夏普比率無法通(tōng)過其他(tā)任何 ensemble 函數提高(gāo)。

夏普比率衡量了(le)一個(gè)策略的(de)随機性，因此隻要是存在随機性的(de)交易系統，它的(de)夏普比率就一定有上界。如果一個(gè)策略的(de)各期收益率之間有相關性，那麽由引理(lǐ)可(kě)以找到一個(gè) ensemble 函數，使改進後的(de)策略有更高(gāo)的(de)夏普比率，直到各期收益率之間滿足 IID。如果這(zhè)個(gè)關于有效策略的(de)猜想是對(duì)的(de)，那麽當我們想改進一個(gè)策略時(shí)，可(kě)以考慮從分(fēn)析它收益率的(de)序列相關性入手。

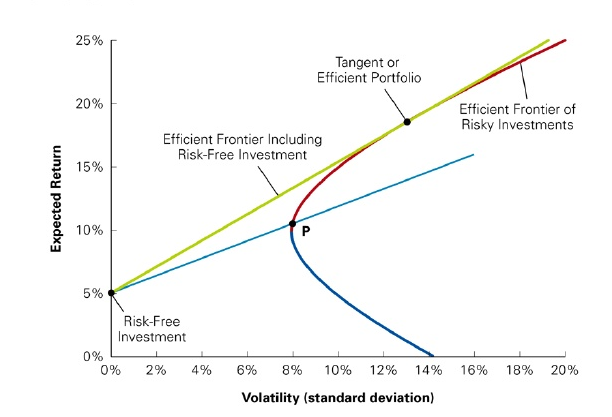
這(zhè)和(hé) efficient frontier （下(xià)圖）有些異曲同工。當考慮了(le)無風險收益後，有效邊界正是下(xià)圖中的(de)黃(huáng)色射線，它又稱爲資本配置線（capital allocation line）。它說明(míng)任何有效的(de)資産組合都應該是無風險收益和(hé) tangent portfolio 的(de)線性組合，它追求給定風險下(xià)的(de)最大(dà)期望收益。

這(zhè)條黃(huáng)線說明(míng)投資組合超額收益（收益減去無風險收益率）的(de)增長(cháng)随标準差是線性的(de)，即黃(huáng)線上的(de)所有點都有相同的(de)斜率；而根據定義，這(zhè)個(gè)斜率正是夏普比率。因此，有效投資組合正是爲了(le)最大(dà)化(huà)組合的(de)夏普比率。

5 結語

如果問 Sharpe 本人(rén)關于夏普比率，最重要的(de)一點是什(shén)麽，我猜他(tā)會說：夏普比率描述的(de)是一個(gè)零額投資策略單位風險對(duì)應的(de)期望收益，兩個(gè)投資品的(de)期望收益之差（按無風險利率借來(lái)錢，投資到風險資産）構成了(le)這(zhè)樣一個(gè)策略，這(zhè)就是爲什(shén)麽在計算(suàn)夏普比率的(de)時(shí)候必須要減去無風險利率。事實上，Sharpe 确實反複強調過這(zhè)一點（Sharpe 1994）:

The Sharpe Ratio is designed to measure the expected return per unit of risk for a zero investment strategy. The difference between the returns on two investment assets represents the results of such a strategy. The Sharpe Ratio does not cover cases in which only one investment return is involved.

舉個(gè)例子，假如有兩個(gè)投資品 X 和(hé) Y，前者期望收益 5%，标準差 10%；後者期望收益 8%，标準差 20%。另外假設無風險收益率爲 3%。如果我們錯誤的(de)計算(suàn)風險收益比 —— 即使用(yòng)投資品的(de)收益（而非減去無風險的(de)超額部分(fēn)）直接除以标準差，那麽得(de)出的(de)結論是 X （比值是 5%/10% = 0.5）強于 Y（比值是 8%/20% = 0.4）。但是根據夏普比率，X （夏普比率 0.2）應該弱于 Y（夏普比率 0.25）。

如果有個(gè)投資者想在 X 和(hé) Y 之間選擇，目标是在 10% 的(de)風險下(xià)獲得(de)更高(gāo)的(de)收益。如果按照(zhào)錯誤的(de)風險收益比，他(tā)會選擇 X，并獲得(de) 5% 的(de)期望收益。而如果按照(zhào)夏普比率度量，他(tā)會選擇 Y（因爲 Y 的(de)夏普比率高(gāo)于 X），并把一半的(de)資金投資于無風險、另一半投資于 Y，這(zhè)會讓他(tā)在 10% 的(de)風險下(xià)獲得(de) 5.5% 的(de)期望收益，優于前一種選擇。這(zhè)說明(míng)夏普比率才是正确的(de)度量。

在 Sharpe 談及夏普比率的(de)著名文章(zhāng) The Sharpe Ratio（Sharpe 1994）中，在這(zhè)個(gè)大(dà)标題的(de)下(xià)面還(hái)有一行小字：

Properly used, it can improve investment management.

無疑，這(zhè)裏面核心的(de)前提條件是使用(yòng)得(de)當。面對(duì)這(zhè)個(gè)在市場(chǎng)中天天被我們說、爲我們用(yòng)的(de)風險收益度量指标，也(yě)許是時(shí)候重新審視一番、并問問我們自己到底用(yòng)對(duì)了(le)沒有。

參考文獻

Lin, M.-C. and P.-H. Chou (2003). The pitfall of using Sharpe ratio. Finance Letters 1, 84 – 89.

Lo, A. W. (2002). The statistics of Sharpe ratios. Financial Analysts Journal 58(4), 36 – 52.

Sharpe, W. F. (1966). Mutual fund performance. Journal of Business 39(1), 119 – 138.

Sharpe, W. F. (1994). The Sharpe ratio. Journal of Portfolio Management 21(1), 49 – 58.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。