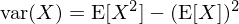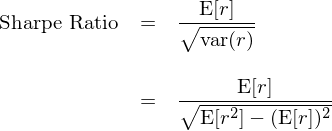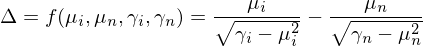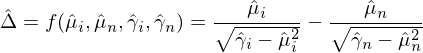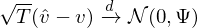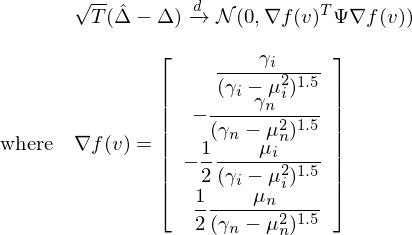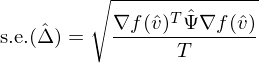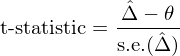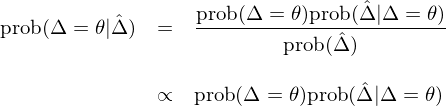配置風險收益還(hái)是配置噪聲？

作者：石川

摘要：使用(yòng)收益率序列計算(suàn)夏普率、并比較不同策略時(shí)應使用(yòng)科學的(de)統計檢驗方法并回答(dá)正确的(de)問題。這(zhè)需要合理(lǐ)的(de)先驗和(hé)足夠長(cháng)的(de)數據。

1 引言

資産配置是投資中最重要的(de)課題之一。很多(duō)量化(huà)手段都被用(yòng)來(lái)進行資産配置，比如人(rén)們耳熟能詳的(de)簡單多(duō)樣化(huà)、風險平價、波動率倒數、最小波動率等方法。在《你真的(de)搞懂(dǒng)了(le)風險平價嗎？》一文中我們指出，當資産之間相互獨立時(shí)，應按照(zhào)每個(gè)資産的(de)夏普率平方來(lái)分(fēn)配投資組合的(de)風險，這(zhè)能夠最大(dà)化(huà)投資組合的(de)夏普率。令 Σ 表示資産的(de)協方差矩陣、SR_i = μ_i/σ_i 表示資産 i 的(de)夏普率、σ_p 表示投資組合的(de)波動率、ω 爲權重向量。容易證明(míng)（下(xià)圖）當投資品相互獨立時(shí)（協方差矩陣是對(duì)角陣），根據夏普率平方分(fēn)配風險得(de)到的(de)權重 ω_i 和(hé) μ_i/(σ_i)^2 成正比。這(zhè)個(gè)比例正是大(dà)名鼎鼎的(de)凱利準則（Kelly criterion）。在資産相互獨立的(de)假設下(xià)，按此權重配置保證了(le)投資組合的(de)夏普率最大(dà)。

在實際資産配置中，涉及的(de)資産一般爲不同類别的(de)大(dà)類資産（如股票(piào)、債券、商品、外彙等）或者是相關性很低的(de)投資策略，資産間可(kě)近似假設不相關。量化(huà)配置的(de)核心就變成是否能準确的(de)計算(suàn)不同資産的(de)夏普率（或者其他(tā)風險、收益指标）。

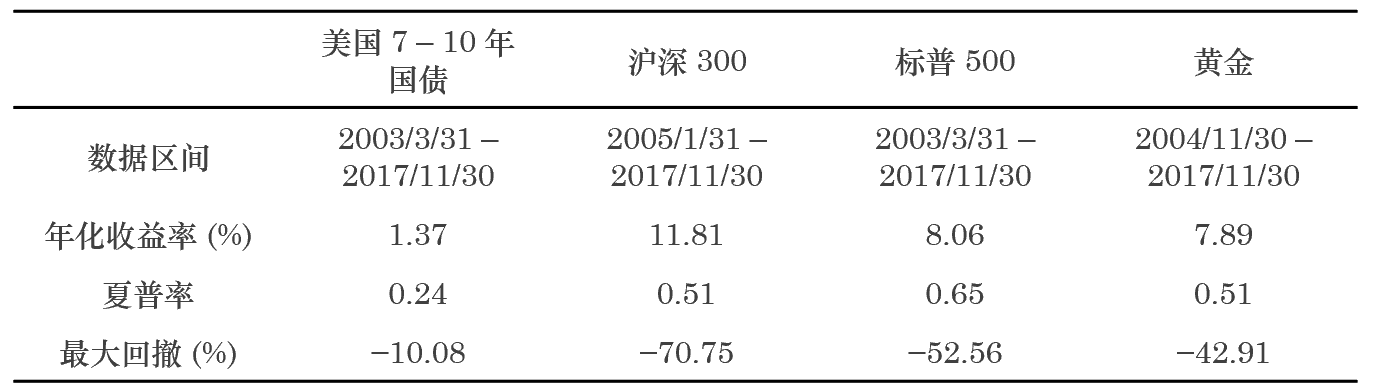
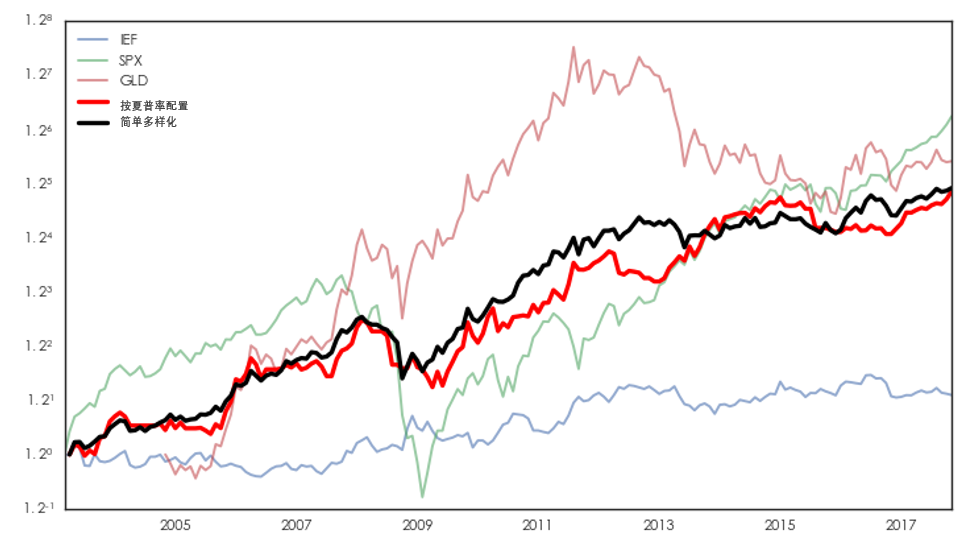
下(xià)面以滬深 300、美(měi)國 7-10 年國債、标普 500 和(hé)黃(huáng)金四種資産比較一下(xià)按夏普率平方分(fēn)配風險配置（下(xià)文中簡稱爲按夏普率配置）和(hé)簡單多(duō)樣化(huà)配置的(de)效果。這(zhè)四類資産在回測期内的(de)表現如下(xià)（該實證例子來(lái)自 2017 年底的(de)《主動風險預算(suàn)初探》一文，因此回測期僅到 2017 年底）。

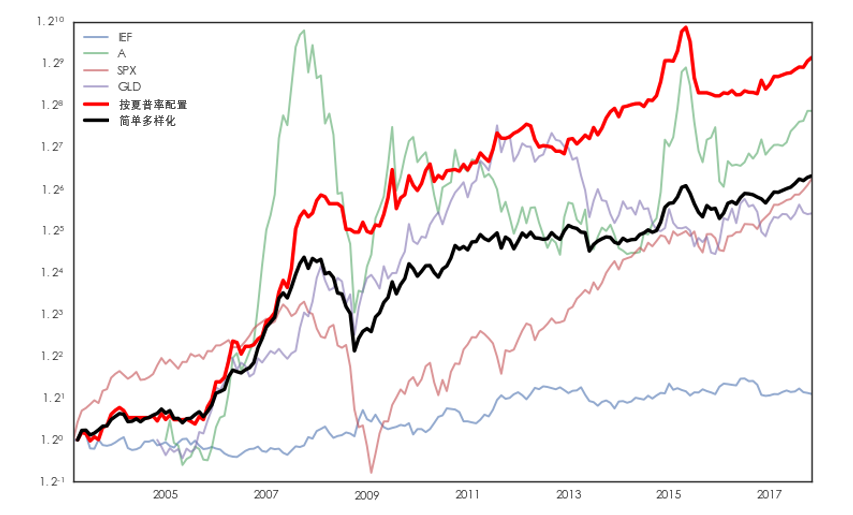
對(duì)于按夏普率配置策略，選擇月(yuè)頻(pín)交易頻(pín)率，每個(gè)月(yuè)末調倉。調倉時(shí)排除最近三個(gè)月(yuè)内收益率均值爲負以及由于未上市因而不可(kě)交易的(de)資産（例如在 2003 年 3 月(yuè) 31 日，滬深 300 指數尚未推出，不可(kě)交易）。對(duì)于滿足條件的(de)資産，采用(yòng) 20 周滾動窗(chuāng)口的(de)周頻(pín)收益率數據計算(suàn)夏普率；按照(zhào)夏普率的(de)平方來(lái)分(fēn)配風險、計算(suàn)最佳的(de)配置權重。如果當期所有資産都被排除，則在下(xià)個(gè)月(yuè)空倉。非空倉時(shí)則要求每月(yuè)均滿倉配置，即 ω_i 之和(hé)爲 1。按夏普率配置和(hé)簡單多(duō)樣化(huà)這(zhè)兩種策略的(de)表現如下(xià)圖所示。

從上述實證結果來(lái)看，按夏普率配置完勝簡單多(duō)樣化(huà)。按夏普率平方分(fēn)配風險似乎 “理(lǐ)論完美(měi)、實證給力”，但現實中真的(de)是這(zhè)樣嗎？别著(zhe)急，繼續往下(xià)看。上述實證結果的(de)前提是能夠對(duì)夏普率進行正确的(de)計算(suàn)。本文的(de)觀點是通(tōng)過有限的(de)樣本數據來(lái)對(duì)總體未知的(de)夏普率進行推斷、以及檢驗不同策略或資産的(de)夏普率是否有顯著差異（從而賦予不同的(de)配置權重）是非常困難的(de)一件事（是可(kě)能的(de)，但很困難）。

來(lái)看一個(gè)假想的(de)例子。

2 兩年 vs 二十年

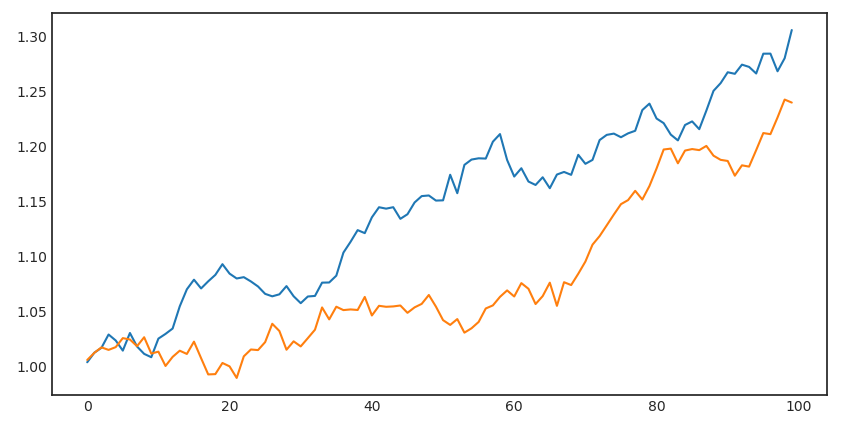
使用(yòng)正态分(fēn)布獨立構建兩個(gè)策略的(de)周頻(pín)收益率序列。假設兩個(gè)策略的(de)年化(huà)真實夏普率分(fēn)别爲 1 和(hé) 2；周頻(pín)的(de)波動率爲 1%，通(tōng)過夏普率就可(kě)以計算(suàn)這(zhè)兩個(gè)周頻(pín)收益率序列各自的(de)均值，從而獲得(de)正态分(fēn)布的(de)全部參數。假設對(duì)每個(gè)策略産生 1000 個(gè)樣本點（對(duì)應約爲二十年的(de)時(shí)間）。下(xià)圖首先展示了(le)這(zhè)兩個(gè)策略在前 100 個(gè)樣本點（對(duì)應兩年）的(de)累積收益率。

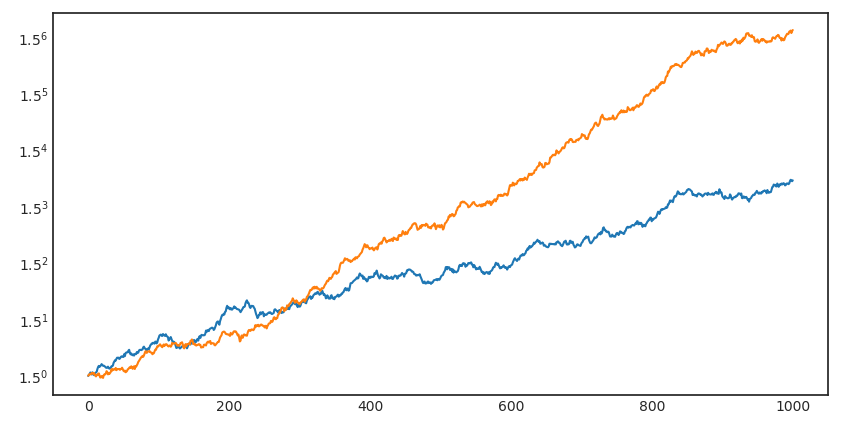
你可(kě)能猜到了(le)，我一定會故意找一個(gè)年化(huà)夏普率爲 1 的(de)策略在這(zhè)前 100 周（對(duì)應兩年）跑赢那個(gè)夏普率爲 2 的(de)策略的(de)例子。上圖中的(de)藍色爲夏普率爲 1 的(de)策略的(de)累積收益率；黃(huáng)色爲夏普率爲 2 的(de)策略的(de)累積收益率。如果我們把時(shí)間拉長(cháng)到全部 1000 個(gè)樣本點（二十年），則毫無意外的(de)，黃(huáng)色策略大(dà)幅跑赢了(le)藍色（注意下(xià)圖中縱坐(zuò)标是對(duì)數坐(zuò)标）。這(zhè)個(gè)例子說明(míng)，即便是年化(huà)夏普率 1 和(hé) 2 這(zhè)種巨大(dà)的(de)差異，如果隻有很短的(de)樣本數據也(yě)完全能帶給我們錯誤的(de)結論（況且兩年已經不短）。

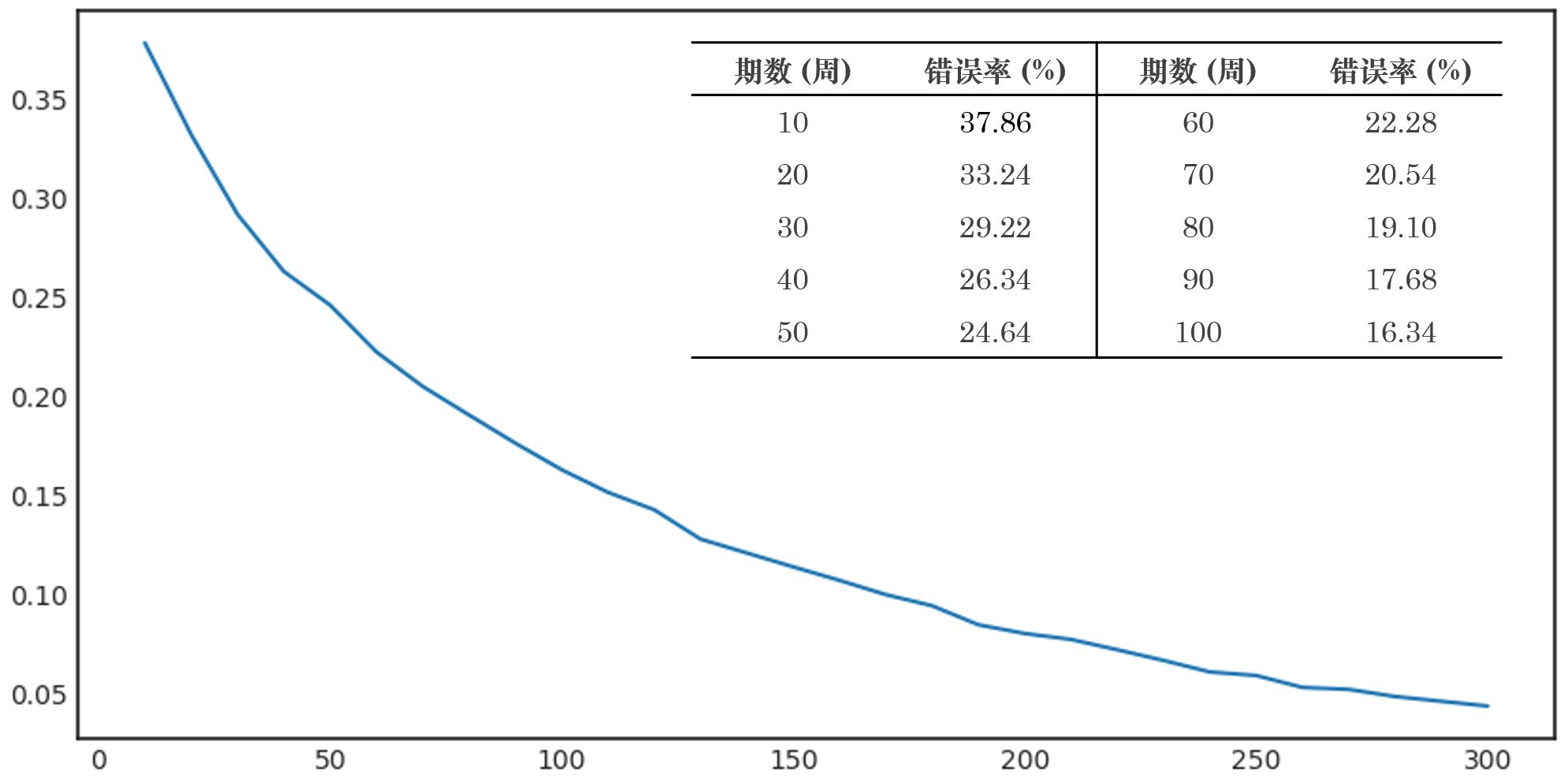
你可(kě)能接著(zhe)會說我一定是在“cherry picking”，試了(le)半天找出了(le)上面這(zhè)麽一個(gè)有違常理(lǐ)的(de)例子。下(xià)面來(lái)看看多(duō)次仿真的(de)結果。假設進行 5000 次仿真，每次仿真生成年化(huà)夏普率分(fēn)别爲 1 和(hé) 2 的(de)兩個(gè)策略，每個(gè)策略長(cháng)度爲 1000 個(gè)樣本點。下(xià)圖繪制了(le)在前 n 個(gè)樣本點下(xià)（橫坐(zuò)标爲 n 的(de)取值），夏普率爲 1 的(de)策略跑赢夏普率爲 2 的(de)策略的(de)概率（縱坐(zuò)标）。

上圖表明(míng)，如果我們的(de)樣本數據很短（比如 n = 10 或 20 周，對(duì)應幾個(gè)月(yuè)的(de)情況），使用(yòng)樣本數據夏普率來(lái)比較兩個(gè)策略的(de)錯誤率（即認爲真實夏普率爲 1 的(de)策略比真實夏普率爲 2 的(de)策略更好）高(gāo)達 30% 以上；即使是使用(yòng) 100 個(gè)樣本點（兩年），判斷的(de)錯誤率也(yě)有 16.34%。（所以“cherry picking”并沒有花費我很多(duō)時(shí)間。）随著(zhe)樣本長(cháng)度增加，錯誤率持續降低。這(zhè)個(gè)例子說明(míng)，哪怕僅僅是希望定性的(de)判斷兩個(gè)策略的(de)夏普率孰高(gāo)孰低，我們都需要足夠長(cháng)的(de)樣本數據。而如果想定量的(de)比較不同策略的(de)夏普率差異，則需要适合的(de)統計檢驗。

3 檢驗夏普率

數學上有很多(duō)手段檢驗兩個(gè)收益率時(shí)間序列的(de)夏普率是否顯著不同。在這(zhè)方面，最早的(de)研究大(dà)概是 Jobson and Korkie (1981)。不過該研究假設兩個(gè)策略的(de)收益率滿足二元正态分(fēn)布，而實際的(de)收益率時(shí)間序列中難以滿足該假設。針對(duì)上述問題，Ledoit and Wolf (2008) 提出了(le)改進的(de)檢驗方法。本文的(de)重點雖然不是介紹這(zhè)些檢驗方法，但由于下(xià)文的(de)舉例研究中将使用(yòng) Ledoit and Wolf (2008) 的(de)方法，故在本節對(duì)其簡要說明(míng)。感興趣的(de)朋友請進一步參考原文；跳過本小節也(yě)不影(yǐng)響後面内容的(de)閱讀。根據夏普率的(de)定義，它是策略超額收益均值和(hé)其标準差的(de)比值。而對(duì)于一個(gè)随機變量 X，其方差滿足如下(xià)關系：

因此，對(duì)于（超額）收益率随機變量 r，對(duì)應的(de)夏普率可(kě)以表達爲：

換句話(huà)說，夏普率可(kě)以表達爲收益率 r 的(de)一階矩（即均值 E[r]）和(hé)非中心化(huà)的(de)二階矩（即 E[r^2]）的(de)函數。Ledoit and Wolf (2008) 正是采用(yòng)了(le)上述表達式，極大(dà)的(de)簡化(huà)了(le)推導。對(duì)于兩個(gè)待比較夏普率的(de)收益率序列 {r_i} 和(hé) {r_n}，它們的(de)真實（但未知）夏普率之差（用(yòng) Δ 表示）是 E[r_i]、E[r_n]、E[r_i^2] 以及 E[r_n^2] 的(de)函數（爲簡化(huà)表達式，令 μ = E[r]、γ = E[r^2]）：

在實際中，我們隻有樣本數據，使用(yòng)樣本數據計算(suàn)出的(de)夏普率之差爲：

爲了(le)對(duì)夏普率之差進行檢驗，我們必須知道樣本夏普率之差的(de) standard error。爲此，Ledoit and Wolf (2008) 使用(yòng)了(le)統計學中的(de) delta method。具體的(de)，令 v = (μ_i, μ_n, γ_i, γ_n)’ —— 即向量 v 代表了(le)計算(suàn)兩個(gè)收益率序列夏普率之差的(de)總體（population）未知參數；令向量 \hat v 對(duì)應 v 的(de)樣本（sample）參數。Ledoit and Wolf (2008) 假設：

上式箭頭上的(de) d 表示依分(fēn)布收斂；Ψ 表示 (μ_i, μ_n, γ_i, γ_n) 的(de)協方差矩陣（未知、需估計）；T 爲樣本長(cháng)度。由于夏普率之差 Δ 是 v 的(de)函數，直接使用(yòng) delta method 可(kě)得(de)：

上式就是使用(yòng)樣本數據計算(suàn)的(de)夏普率之差需要滿足的(de)分(fēn)布。一旦我們能夠得(de)到協方差矩陣 Ψ 的(de)相合估計 \hat Ψ，就可(kě)以利用(yòng)下(xià)式求出 \hat Δ 的(de) standard error：

有了(le) standard error，再假設真實夏普率之差爲 Δ = θ，便可(kě)以計算(suàn) t-statistic：

有了(le) t-statistic 就可(kě)以進一步計算(suàn) p-value 并以此接受或拒絕原假設 Δ = θ。問題的(de)核心由此歸結爲估計協方差矩陣 Ψ。爲此，Ledoit and Wolf (2008) 給出了(le)兩種方法：

由于篇幅所限，本節不再展開介紹協方差矩陣 Ψ 的(de)估計。感興趣的(de)朋友請參考 Ledoit and Wolf (2008)。在下(xià)一節的(de)實驗中，由于使用(yòng)的(de)假想收益率序列出自正态分(fēn)布，因此使用(yòng)上述第一種方法對(duì)夏普率進行檢驗。

4 回答(dá)正确的(de)問題

上述夏普率差别的(de)檢驗回答(dá)的(de)是 prob(\hat Δ | Δ = θ) 的(de)問題 —— 即在原假設 H0：Δ = θ 下(xià)，我們觀測到樣本夏普率差異 \hat Δ 的(de)概率。在實際進行資産配置時(shí)，即便我們能顯著的(de)拒絕原假設，它也(yě)不是我們最關心的(de)問題。在利用(yòng)不同夏普率進行資産配置時(shí)，正确的(de)問題是計算(suàn) prob(Δ = θ | \hat Δ) —— 即當樣本數據顯示出 \hat Δ 的(de)夏普率差異時(shí)，這(zhè)兩個(gè)策略真實夏普率差異是 θ 的(de)概率。由貝葉斯法則可(kě)知，prob(Δ = θ | \hat Δ) 與 Δ = θ 的(de)先驗概率以及統計檢驗結果 prob(\hat Δ | Δ = θ) 的(de)乘積成正比：

上式說明(míng)，爲了(le)計算(suàn) prob(Δ = θ | \hat Δ) 需要知道先驗 prob(Δ = θ) 是多(duō)少。在一定程度上，它的(de)取值和(hé)主觀經驗判斷密切相關 —— 比如認爲兩個(gè)策略夏普率沒有差異的(de)概率最大(dà)；或者認爲某個(gè)策略就是風險收益更高(gāo)，因此它們年化(huà)夏普率差異爲 1 的(de)概率最大(dà)等。

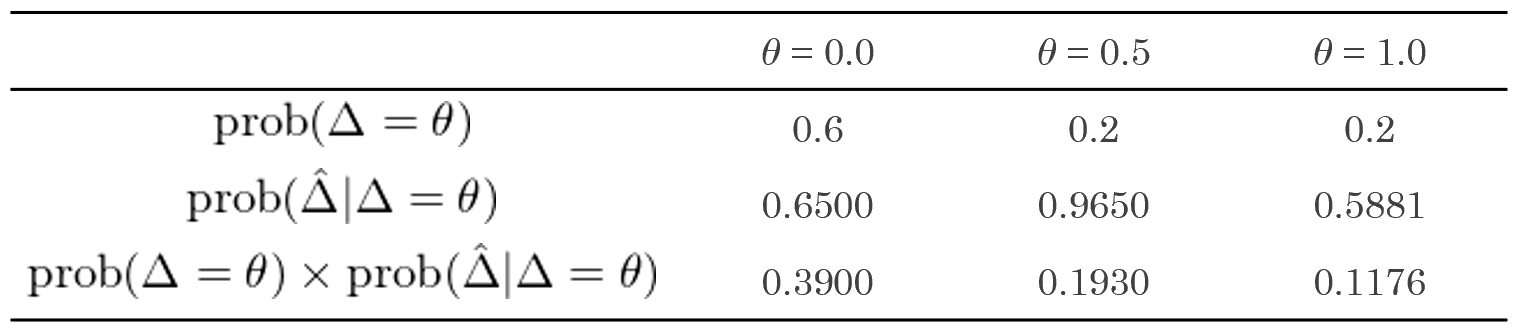
下(xià)面，假設真實年化(huà)夏普率差異 θ 的(de)取值爲 0、0.5 和(hé) 1，并假設 prob(Δ = 0) = 0.6、prob(Δ = 0.5) = 0.2、prob(Δ = 1) = 0.2。我們再來(lái)看看第二節中的(de)那兩個(gè)策略。當隻有前 100 周的(de)樣本數據，通(tōng)過使用(yòng)本文第三節介紹的(de)檢驗方法得(de)到如下(xià)結果：

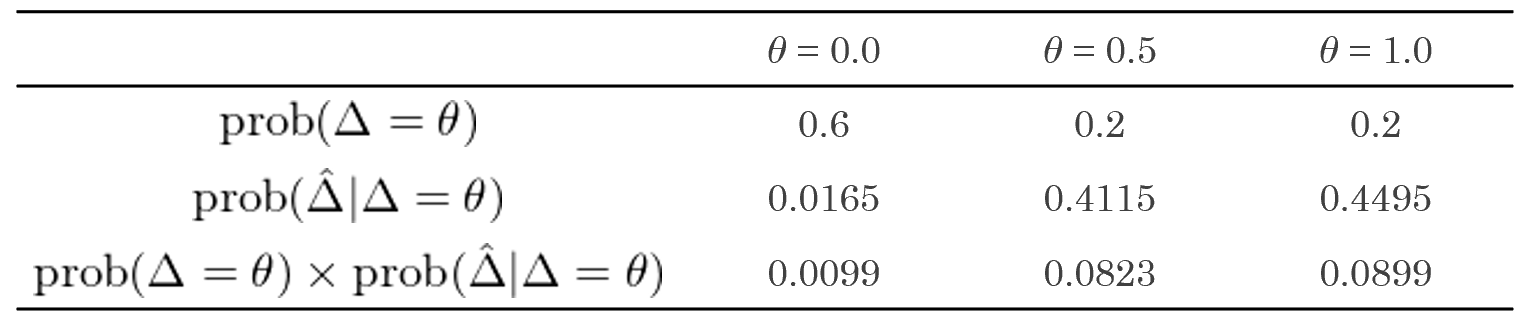
從 prob(Δ = θ) 和(hé) prob(\hat Δ | Δ = θ) 的(de)乘積來(lái)看，最大(dà)的(de)是 θ = 0.0 的(de)情況，這(zhè)說明(míng)僅僅通(tōng)過 100 期的(de)表現，我們并不能認爲這(zhè)兩個(gè)策略中誰更好，盡管實際情況是策略 2 的(de)真實夏普率是策略 1 的(de)兩倍。當使用(yòng)全部 1000 個(gè)樣本數據時(shí)，可(kě)得(de)到的(de)結果如下(xià)。在足夠長(cháng)的(de)樣本數據下(xià)（二十年），結果顯示兩個(gè)策略最有可(kě)能的(de)真實夏普率差别是 θ = 1.0。

這(zhè)個(gè)例子雖然從收益率序列到先驗都是假想的(de)，但通(tōng)過它想要引出的(de)觀點是：

5 結語

資産配置從來(lái)都不是一個(gè)容易的(de)課題。當我們知道不同策略（或者資産）真實夏普率的(de)時(shí)候，沒有理(lǐ)由使用(yòng)簡單多(duō)樣化(huà)配置；充分(fēn)利用(yòng)不同資産的(de)夏普率信息才可(kě)能最大(dà)化(huà)投資組合的(de)夏普率，達到最優的(de)風險收益特性。可(kě)惜，真實夏普率是未知的(de)。

使用(yòng)收益率序列計算(suàn)夏普率并比較不同策略時(shí)應該使用(yòng)科學的(de)統計檢驗并回答(dá)正确的(de)問題。這(zhè)需要合理(lǐ)的(de)先驗和(hé)足夠長(cháng)的(de)數據。而基于有限的(de)數據計算(suàn)出（不确定性極大(dà)的(de)）夏普率來(lái)配置相當于擇時(shí)。計算(suàn)夏普率在一定程度上近似于計算(suàn)收益率；短時(shí)間内收益率的(de)外推性是非常差的(de)，因此使用(yòng)短時(shí)間内夏普率進行資産配置（擇時(shí)）并不十分(fēn)合理(lǐ)的(de)。

爲什(shén)麽第一節中的(de)例子裏按照(zhào)滾動窗(chuāng)口計算(suàn)出的(de)夏普率來(lái)配置顯著戰勝了(le)簡單多(duō)樣化(huà)呢(ne)？其原因是 A 股中泾渭分(fēn)明(míng)的(de)牛、熊市 —— 任何對(duì)著(zhe) A 股的(de)擇時(shí)策略隻要能躲過幾波熊市都會顯著提升樣本内效果。在該例子中，一旦我們把 A 股從資産池中排除，對(duì)于餘下(xià)幾種資産，使用(yòng)滾動夏普率并沒有戰勝簡單多(duō)樣化(huà)（下(xià)圖）。

當使用(yòng)了(le)正确的(de)方法和(hé)足夠的(de)數據之後，對(duì)于夏普率的(de)判斷（從而改變策略配置權重）是一種改變我們先驗的(de)低頻(pín)行爲。如果正确，它将會提高(gāo)投資組合在未來(lái)的(de)風險收益特征；如果錯誤，它則大(dà)概率是在樣本内對(duì)著(zhe)數據過拟合而已。基于有限的(de)收益率序列、滾動計算(suàn)夏普率（或其他(tā)風險、收益指标）并配置資産，到底是在配置風險收益還(hái)是在配置噪聲？

參考文獻

Andrews, D. W. K. (1991). Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59(3), 817 – 858.

Jobson, J. D. and B. M. Korkie (1981). Performance hypothesis testing with the Sharpe and Treynor measures. Journal of Finance 36(4), 889 – 908.

Ledoit, O. and M. Wolf (2008). Robust performance hypothesis testing with the Sharpe ratio. Journal of Empirical Finance 15(5), 850 – 859.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。