Farewell，ad-hoc 多(duō)因子模型

發布時(shí)間：2022-01-28 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：強加人(rén)爲稀疏性假設的(de)多(duō)因子模型注定會成爲一段曆史，但以它們爲基礎也(yě)會孕育出新的(de)範式。

1 引言

前文《稀疏性幻覺》曾抛出這(zhè)樣的(de)觀點，在以往被提出的(de)、如今早已成爲實證資産定價中占主導地位的(de)諸多(duō)多(duō)因子模型都帶有非常強的(de)稀疏性假設。這(zhè)背後的(de)動機是繞過和(hé)收益率有關的(de)協變量的(de)高(gāo)維數問題，從而用(yòng)低維模型研究定價問題。然而，希望通(tōng)過包含有限個(gè)因子的(de) ad-hoc 多(duō)因子模型來(lái)解釋股票(piào)預期收益率或者 span 出更大(dà)的(de)夏普比率平方，僅僅是一種稀疏性幻覺。雖然追求簡約模型本身并無不妥，但這(zhè)些曆史上曾經輝煌一時(shí)的(de)模型并非實證資産定價的(de)未來(lái)，也(yě)終将退出曆史的(de)舞台。本文借 Cooper et al. (2021) 一文，從 APT 的(de)角度針對(duì)上述觀點再來(lái)做(zuò)一番探討(tǎo)。

2 APT 與 PCA

關于 APT（Ross 1976）的(de)經濟學動機，Cochrane (2005) 有如下(xià)描述：Factor structure can imply factor pricing (APT). The APT suggests that one start with a statistical analysis of the covariance matrix of returns and find portfolios that characterize common movement. 這(zhè)段話(huà)的(de)意思就是，能夠解釋資産收益率共同運動的(de)因子也(yě)應該是能夠解釋資産預期收益率截面差異的(de)因子。在市場(chǎng)中不存在近似無風險套利機會這(zhè)個(gè)假設下(xià)，Kozak, Nagel, and Santosh (2018) 同樣論述了(le)這(zhè)一點（見《Which beta (III)?》）。這(zhè)個(gè)經濟學動機也(yě)正是最近幾年利用(yòng) PCA 構造隐性因子模型備受關注的(de)原因。這(zhè)也(yě)是本節的(de)題目爲 APT 與 PCA 的(de)原因。我們再從數學上簡單看一下(xià)。假設資産的(de)超額收益滿足如下(xià)回歸模型：

$R^e_{i}=a_i+\beta_{i,1}\tilde{F}_{1}+\cdots+\beta_{i,K}\tilde{F}_{K}+\varepsilon_{i}.$

其中 $R^e_{i}$ 是資産的(de)超額收益， $\tilde{F}_{k}\equiv F_k-\mbox{E}[F_k], k=1,\cdots,K$ 是 demean 之後的(de)因子（因子可(kě)以是 traded portfolios，即我們熟悉的(de) long/short portfolio returns，也(yě)可(kě)以是 nontraded portfolios）。由于在上式中對(duì)因子取值做(zuò)了(le)去均值處理(lǐ)，因此有 $\mbox{E}[R^e_i]=a_i$ 。接下(xià)來(lái)，令 $M$ 表示随機貼現因子（SDF）。由于 $R^e_i$ 表示超額收益，因此有 $\mbox{E}[MR^e_i]=0$ 。對(duì)上面的(de)回歸模型兩邊同時(shí)乘以 $M$ 并求期望可(kě)得(de)：

0=a_i\mbox{E}[M]+\beta_{i,1}\mbox{E}[M\tilde{F}_{1}]+\cdots+\beta_{i,K}\mbox{E}[M\tilde{F}_{K}]+\mbox{E}[M\varepsilon_{i}].

利用(yòng) $\mbox{E}[R^e_i]=a_i$ ，将 $\mbox{E}[R^e_i]$ 替換上式中的(de) $a_i$ 并做(zuò)簡單運算(suàn)：

$\mbox{E}[R^e_i]=-\beta_{i,1}\frac{\mbox{E}[M\tilde{F}_{1}]}{\mbox{E}[M]}-\cdots-\beta_{i,K}\frac{\mbox{E}[M\tilde{F}_{K}]}{\mbox{E}[M]}-\frac{\mbox{E}[M\varepsilon_{i}]}{\mbox{E}[M]}.$

定義 $\lambda_k\equiv-\mbox{E}[ M\tilde{F}_k]/\mbox{E}[M]$ 以及 $\alpha_i\equiv-\mbox{E}[M\varepsilon_i]/\mbox{E}[M]$ ，上式最後變成我們熟悉的(de)形式：

$\mbox{E}[R^e_i]=\alpha_i+\beta_{i,1}\lambda_1+\cdots+\beta_{i,K}\lambda_K.$

可(kě)以證明(míng)，當因子是 traded portfolio returns 時(shí)， $\lambda_i=\mbox{E}[F_i]$ 。在 APT 的(de)推導中，隐含的(de)假設是不同資産的(de) $\varepsilon_{i}$ 是相互獨立的(de)，即 $\mbox{E}[\varepsilon_{i}\varepsilon_{j}]=0$ ，且特質收益率的(de)方差 $\mbox{var}(\varepsilon_{i})$ 是有界的(de)。在這(zhè)兩個(gè)條件下(xià)，如果利用(yòng)本節的(de)回歸模型計算(suàn)不同資産超額收益率之間的(de)協方差矩陣，則一個(gè)自然的(de)結果就是這(zhè)些解釋資産預期收益率的(de)因子同時(shí)也(yě)能解釋資産的(de)協方差矩陣。在這(zhè)個(gè)結論下(xià)，APT 爲我們比較不同 ad-hoc 多(duō)因子模型提供了(le)一個(gè)天然的(de)基準 —— 我們可(kě)以通(tōng)過 PCA 分(fēn)解資産的(de)協方差矩陣，利用(yòng)特征向量作爲權重構造“統計”因子投資組合，以這(zhè)些組合的(de)收益率爲因子構造一個(gè)基準的(de)多(duō)因子模型。

如果 ad-hoc 模型能夠比較好的(de)描述投資者在市場(chǎng)中面對(duì)的(de)投資機會以及不同資産截面預期收益率的(de)差異，則它們在資産定價方面的(de)表現和(hé)上述基于 PCA 的(de)基準模型之間不應該存在統計上顯著的(de)差異。以此爲出發點，就能夠評價不同的(de) ad-hoc 多(duō)因子模型。這(zhè)也(yě)正是 Cooper et al. (2021) 的(de)研究動機。

3 實證結果

雖然理(lǐ)論很清晰，但是實證依然充滿挑戰，那就是基于哪個(gè)協方差矩陣構造基準模型。在這(zhè)方面，使用(yòng)個(gè)股是不現實的(de)，所以隻能取而代之使用(yòng)常見的(de) sorted portfolios 作爲資産。Cooper et al. (2021) 基于數據可(kě)得(de)性等原因選擇了(le) 42 個(gè)常見的(de)異象，并通(tōng)過每個(gè)異象變量将股票(piào)分(fēn)成 10 組（每月(yuè)再平衡），一共得(de)到了(le) 420 個(gè)投資組合。以它們爲資産計算(suàn)協方差矩陣，Cooper et al. (2021) 構造了(le)一個(gè)包含 6 個(gè)主成分(fēn)的(de)基準模型，記爲 APT6。再來(lái)看看被評價的(de) ad-hoc 多(duō)因子模型。該文一共考慮了(le) 7 個(gè)模型，都是人(rén)們非常熟悉的(de)，見下(xià)表。

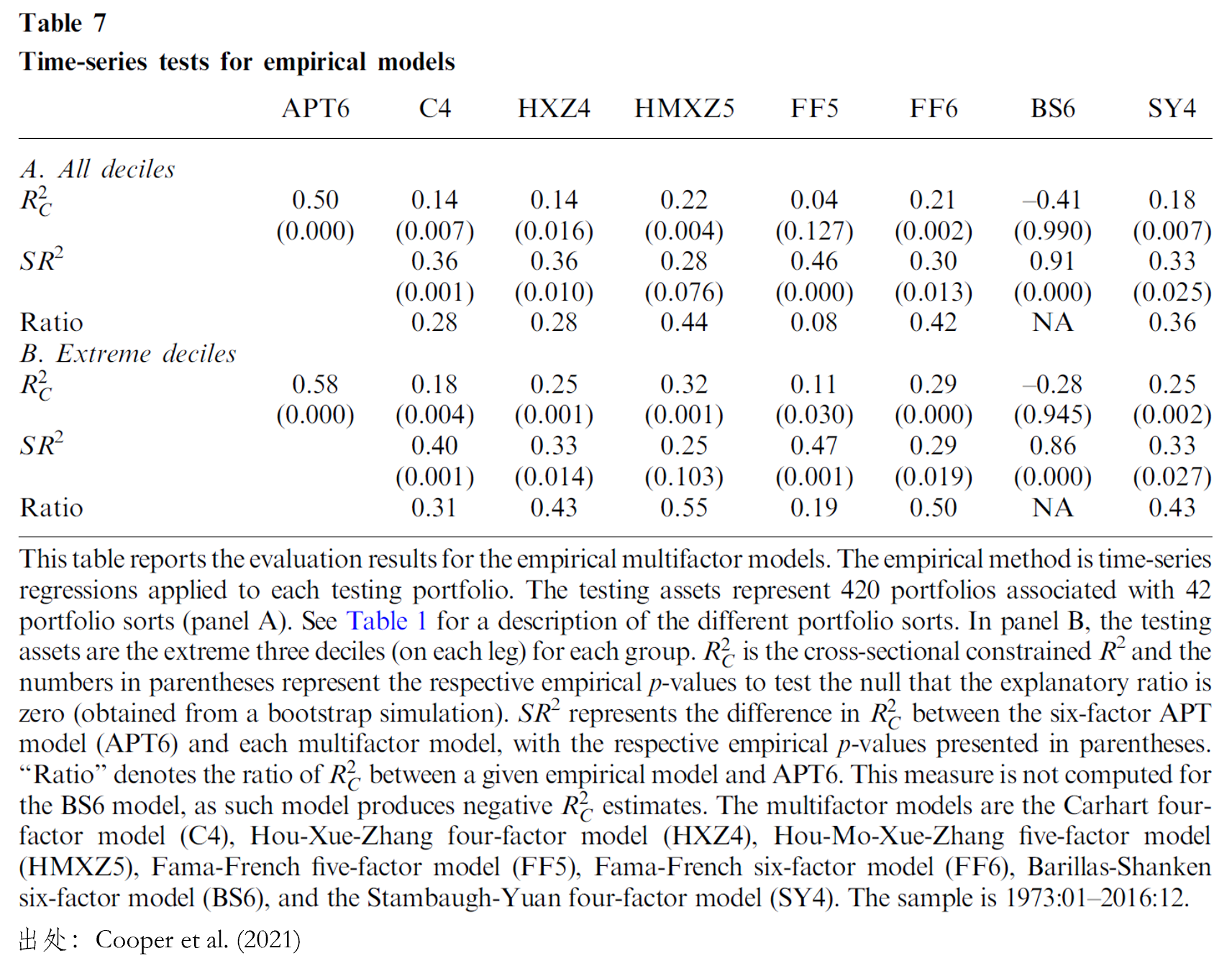
爲了(le)比較來(lái)自 APT 的(de)基準模型和(hé)上述 7 個(gè) ad-hoc 模型，Cooper et al. (2021) 使用(yòng)了(le)很多(duō)常見的(de)實證資産定價檢驗手段。本節介紹其中一個(gè)，即 time-series spanning test。以上述 420 個(gè) sorted portfolios 作爲 test assets，分(fēn)别對(duì)這(zhè) 8 個(gè)模型進行時(shí)序回歸，計算(suàn)每個(gè) test asset 的(de) pricing error，并基于 pricing errors 進行檢驗。其中一個(gè)檢驗統計量是截面 R-squared，定義如下(xià)：

$R_c^2=1-\frac{\mbox{var}(\alpha_i)}{\mbox{var}(\bar{R}_i^e)}.$

其中 $\mbox{var}(\alpha_i)$ 是 test assets 的(de) pricing errors 在截面上的(de)方差， $\mbox{var}(\bar{R}_i^e)$ 是這(zhè)些資産的(de)平均收益率在截面上的(de)方差。由定義可(kě)知， $R_c^2$ 越大(dà)則說明(míng)模型解釋資産預期收益率的(de)能力越強。下(xià)表給出了(le)檢驗結果（隻需要看 Panel A 即可(kě)）。

從 Panel A 可(kě)知，來(lái)自 APT 的(de)基準模型的(de) $R_c^2$ 高(gāo)于任意一個(gè) ad-hoc 模型的(de) $R_c^2$ 。此外， $SR^2$ （請注意它不代表夏普比率平方）這(zhè)一行展示了(le)基準模型和(hé)單個(gè) ad-hoc 模型的(de) $R_c^2$ 之差，其下(xià)方括号内爲對(duì)應的(de) p-value。從 Panel A 的(de)結果可(kě)知，除了(le) HMXZ5 之外，其他(tā) ad-hoc 模型和(hé)基準模型相比的(de)差異均在 5% 的(de)顯著性水(shuǐ)平以下(xià)。而 HMXZ5 和(hé)基準模型的(de)差異的(de)顯著性水(shuǐ)平是 10% 以下(xià)。另外讓人(rén)驚訝的(de)是 BS6 模型的(de) $R_c^2$ 是負的(de)。（Panel B 的(de)穩健性檢驗給出了(le)類似的(de)結果。）

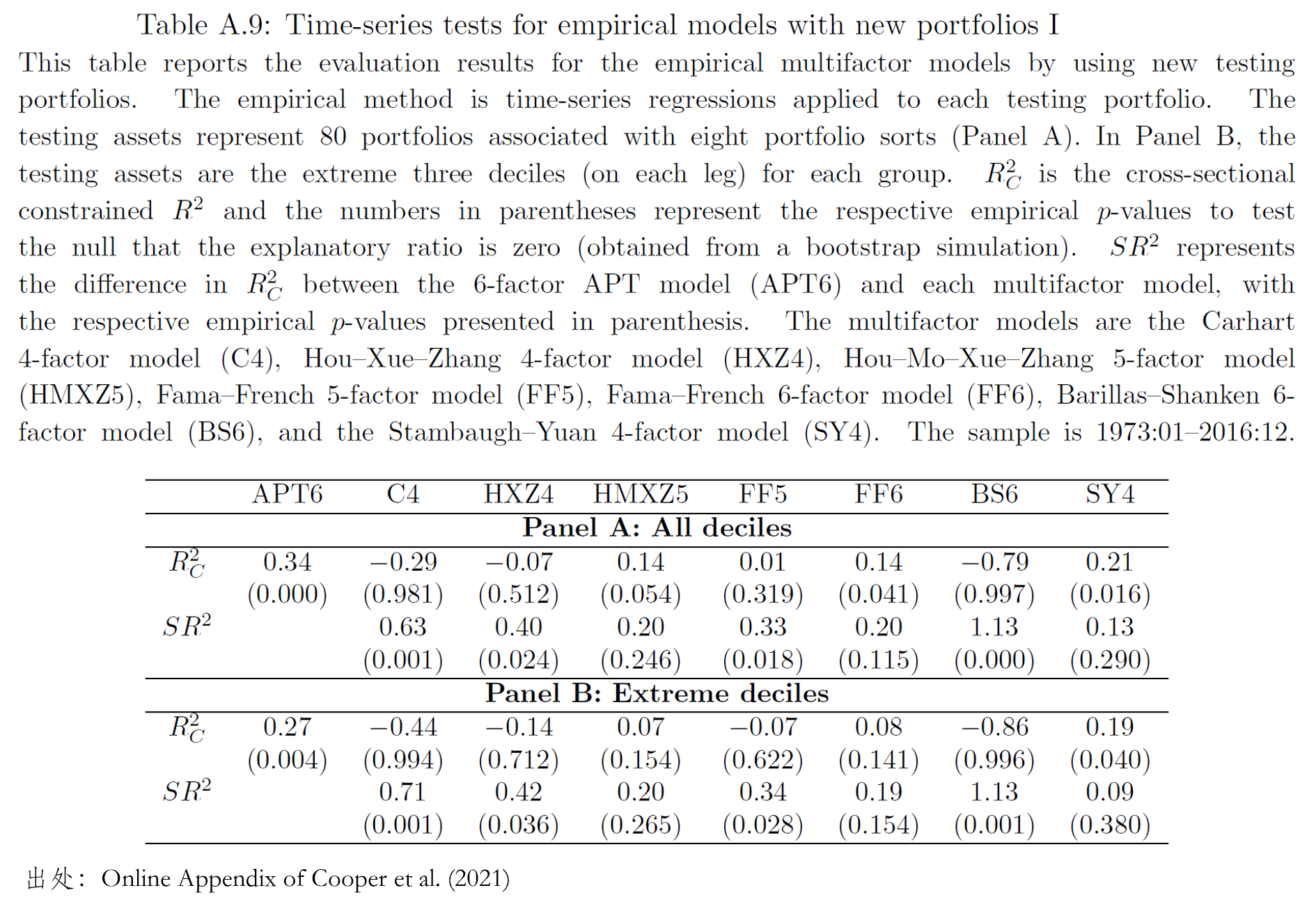
面對(duì)以上實證結果，我們似乎還(hái)不能馬上否定 ad-hoc 模型。其背後的(de)原因有兩個(gè)。首先，APT 模型是根據 420 個(gè)作爲 test assets 的(de)協方差矩陣構造的(de)，它是一個(gè)純粹的(de) in-sample test，它能解釋更多(duō)的(de)截面差異理(lǐ)所應當。第二，HMXZ5 這(zhè)個(gè)最近兩年出盡風頭的(de)模型（見 Hou et al 2019）和(hé) APT 模型的(de)差距在統計上并不是那麽顯著。不過值得(de)一提的(de)是，HMXZ5 雖然源自加強版的(de) q-theory model（見《從 Factor Zoo 到 Factor War，實證資産定價走向何方？》），但它也(yě)僅僅是事後的(de) in-sample 實證分(fēn)析。爲了(le)排除顧慮，使用(yòng)未被用(yòng)于構造 APT 模型的(de) test assets 就顯得(de)格外重要。爲此，Cooper et al. (2021) 使用(yòng)了(le)另外 8 個(gè)異象構造了(le) 80 個(gè) sorted portfolios 作爲 test assets。結果如下(xià)。

對(duì)于這(zhè) 80 個(gè) test assets 來(lái)說，基準模型 APT6 依然有不錯的(de)定價能力，其 $R_c^2$ 爲0.34（p-value = 0.000）。反觀各種 ad-hoc 模型，C4、HXZ4 以及 BS6 的(de) $R_c^2$ 均爲負。其中表現最好的(de)是 SY4。另外，雖然以定價能力差異來(lái)看，我們依然不能說 HMXZ5（此外這(zhè)回還(hái)有 FF6）和(hé)基準模型的(de)差異在統計上是顯著的(de)，但如果對(duì)照(zhào)著(zhe) $R_c^2$ 來(lái)看，HMXZ5 首先就沒有表現出統計上顯著的(de)定價能力。另外，考慮到 HMXZ5 是 HXZ4 的(de)拓展（僅僅加上了(le)額外的(de)預期投資增長(cháng)因子），我們也(yě)無法忽視 HXZ4 和(hé) HMXZ5 的(de)巨大(dà)反差（ $R_c^2$ 一正一負）。

除本節介紹的(de)實證結果之外，Cooper et al. (2021) 還(hái)考慮了(le)其他(tā)很多(duō)穩健性檢驗，感興趣的(de)小夥伴請閱讀原文。總體而言，來(lái)自 APT 的(de)基準模型無論在 in-sample test 還(hái)是在 out-of-sample test 都表現出了(le)更好的(de)定價能力，因而優于各類 ad-hoc 模型。在諸多(duō) ad-hoc 模型中，唯一能與其相比的(de)是 HMXZ5，但其所代表的(de)投資機會遜于 APT 模型。

4 結束語

最近幾年，實證資産定價的(de)研究範式已從 ad-hoc 多(duō)因子模型轉到隐性多(duō)因子模型，其中的(de)代表作當屬基于 PCA 方法的(de) Kelly, Pruitt, and Su (2019) 以及 Kozak, Nagel, and Santosh (2020)。（順便一提，這(zhè)兩篇文章(zhāng)分(fēn)别獲得(de) 2019 和(hé) 2020 JFE Fama-DFA best paper prize。）無論從對(duì)資産的(de)定價能力，還(hái)是從構造的(de)最大(dà)夏普比率平方來(lái)說，隐性因子模型都要優于 ad-hoc 多(duō)因子模型，一如 Cooper et al. (2021)。對(duì)于業界的(de)投資實務來(lái)說，多(duō)因子模型的(de)作用(yòng)找到最能解釋資産預期收益率差異（即最能代表投資機會）的(de)因子，并最大(dà)化(huà)樣本外的(de)條件風險收益特征。而從實證資産定價來(lái)說，多(duō)因子模型的(de)新範式應能夠正面應對(duì)協變量（公司特征）的(de)高(gāo)維數問題，在摒棄稀疏性假設的(de)前提下(xià)研究衆多(duō)高(gāo)度相關的(de)協變量和(hé)資産收益率的(de)關系。

在可(kě)以預見的(de)未來(lái)，無論是對(duì)業界還(hái)是學界的(de)目标，曾經輝煌一時(shí)的(de) ad-hoc 多(duō)因子模型似乎都無法繼續發揮太大(dà)的(de)作用(yòng)。雖然這(zhè)些模型讓多(duō)因子模型的(de)概念深入人(rén)心，但随著(zhe)理(lǐ)論和(hé)實證資産定價研究持續發展，終有那麽一個(gè)時(shí)刻，我們要對(duì)它們說聲拜拜。也(yě)許這(zhè)個(gè)時(shí)刻已經到來(lái)。

參考文獻

Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton University Press.

Cooper, I., L. Ma, P. Miao, and D. Philip (2021). Multifactor models and their consistency with the APT. Review of Asset Pricing Studies 11(2), 402 – 444.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2018). Choosing factors. Journal of Financial Economics 128(2), 234 – 252.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.

Hou, K., H. Mo, C. Xue, and L. Zhang (2021). An augmented q-factor model with expected growth. Review of Finance 25(1), 1 – 41.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Farewell，ad-hoc 多(duō)因子模型