尋找 Mean-Variance Frontier (II)
發布時(shí)間:2022-04-08 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:實證層面,我們也(yě)許永遠(yuǎn)找不到“最優”的(de) MVE 組合,但理(lǐ)論的(de)突破和(hé)實證的(de)推進對(duì)投資實務而言依然非常有益。
Any asset pricing model is the same as the statement that there is some return on the mean-variance frontier.
—— Cochrane (2005)
1
最近幾年,機器學習(xí)在實證資産定價方面的(de)應用(yòng)愈加深入。學術界提出了(le)很多(duō)利用(yòng)機器學習(xí)方法構造的(de)隐性多(duō)因子模型,例如 Kelly, Pruitt and Su (2019) 的(de) IPCA 模型、Chen, Pelger and Zhu (2019) 的(de)深度學習(xí)模型、Kozak, Nagel and Santosh (2020) 的(de) PCA方法、Bryzgalova, Pelger and Zhu (2020) 的(de)随機森林(lín)方法、以及 Gu, Kelly and Xiu (2021) 的(de) autoencoder 模型等。
和(hé)傳統的(de) Fama and French (1993, 2015) 以及 Hou, Xue and Zhang (2015) 模型相比,這(zhè)些新方法沒有強加 ad-hoc 稀疏性假設,而是選擇直面協變量(公司特征)的(de)高(gāo)維數問題。實證結果顯示,新模型均能獲得(de)傳統模型無法解釋的(de)超額收益,且它們在樣本外 span 出的(de)最大(dà)夏普比率也(yě)遠(yuǎn)超傳統模型。
雖說每個(gè)新模型都能遠(yuǎn)勝傳統模型,但我們并不清楚這(zhè)些新模型之間又會是孰優孰劣。是否會有某個(gè)機器學習(xí)方法構造的(de)模型會優于其他(tā)模型?回答(dá)這(zhè)個(gè)問題的(de)意義絕非“factor (model) war”的(de)升級版,而是對(duì)理(lǐ)論和(hé)實證、對(duì)學界和(hé)業界都意義重大(dà)。
直到 Baba-Yara, Boyer and Davis (2021) 出現。
該文把傳統模型和(hé)基于機器學習(xí)方法構造的(de)新模型放在一起進行了(le)比較。然而有意思的(de)是,該文通(tōng)過詳盡的(de)實證分(fēn)析發現沒有哪個(gè)新模型是“最優”的(de)。正因如此,三位作者給論文的(de)題目選爲 The factor model failure puzzle(在更早先的(de)版本中,該文的(de)标題爲 Evaluating the anomaly zookeepers)。
那麽出現上述現象背後的(de)原因是什(shén)麽呢(ne)?是機器學習(xí)領域中“沒有免費的(de)午餐”定理(lǐ)?又或者是什(shén)麽其他(tā)的(de)原因?Baba-Yara, Boyer and Davis (2021) 的(de)創新之處在于不止進行了(le)實證分(fēn)析,而是通(tōng)過理(lǐ)論模型解釋了(le)上述現象背後的(de)原因。他(tā)們把這(zhè)個(gè)現象稱爲 Impossibility result。
2
爲了(le)合理(lǐ)地比較不同的(de)模型,我們首先來(lái)借助一些理(lǐ)論的(de)指引。實證資産定價理(lǐ)論表明(míng)了(le)(線性)随機貼現因子、多(duō)因子模型以及均值方差有效(MVE)投資組合之間的(de)等價關系。此外,一旦我們找到 mean-variance frontier 上的(de)一個(gè)組合,就可(kě)以用(yòng)它構造一個(gè)單因子模型,并通(tōng)過它來(lái)爲其他(tā)任意資産定價(Roll 1977):
上述結果爲我們比較不同的(de)模型指明(míng)了(le)方向。對(duì)于不同的(de)模型,我們隻需要利用(yòng)它們的(de)因子構造出各自的(de) MVE 投資組合,然後考察這(zhè)些 MVE 組合是否能夠爲彼此定價。如果某個(gè)模型是“最優”模型,則意味著(zhe)其他(tā)模型的(de) MVE 組合無法獲得(de)相較于該模型 MVE 組合的(de)超額收益。
當然,上述“隻需要”背後隐含著(zhe)巨大(dà)的(de)實證挑戰。這(zhè)是因爲我們在乎的(de)是在樣本外構造 MVE 組合,而非在樣本内進行事後分(fēn)析。對(duì)于後者,我們隻需要使用(yòng)
利用(yòng)因子權重,就可(kě)以構造 MVE 組合;而一旦有了(le)所有模型各自的(de) MVE 組合,接下(xià)來(lái)隻需要令它們互爲 test assets 和(hé)基準模型進行回歸分(fēn)析,求出每個(gè) test assets 相對(duì)選定基準(即某個(gè)因子模型的(de) MVE 組合)的(de)超額收益
3
下(xià)面我們來(lái)看看參加 PK 的(de)各路選手。
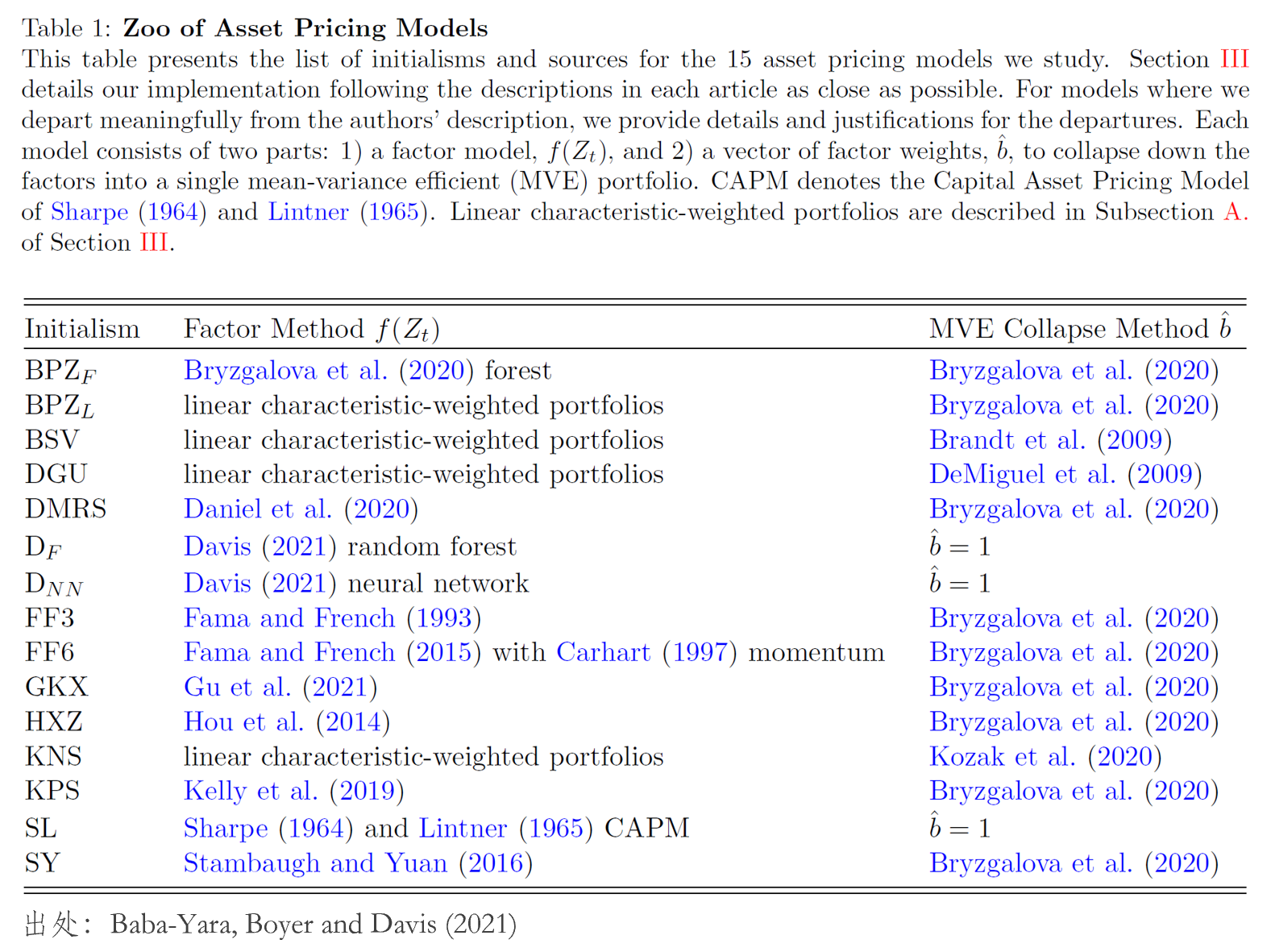
首先是傳統選手,包括 CAPM、FF3(Fama and French 1993)、FF6(Fama and French 2015 + Mom)、HXZ(Hou, Xue and Zhang 2015)、DMRS(Daniel et al. 2020 通(tōng)過對(duì)沖後構造的(de)因子,詳見此處)以及 SY(Stambaugh and Yuan 2016)。至于通(tōng)過機器學習(xí)方法構造的(de)新模型,主要就是本文一開始提到的(de)那些,不再贅述。下(xià)表總結了(le) Baba-Yara, Boyer and Davis (2021) 考察的(de)全部模型以及每個(gè)模型所使用(yòng)的(de)用(yòng)于估計 MVE 權重的(de)方法。
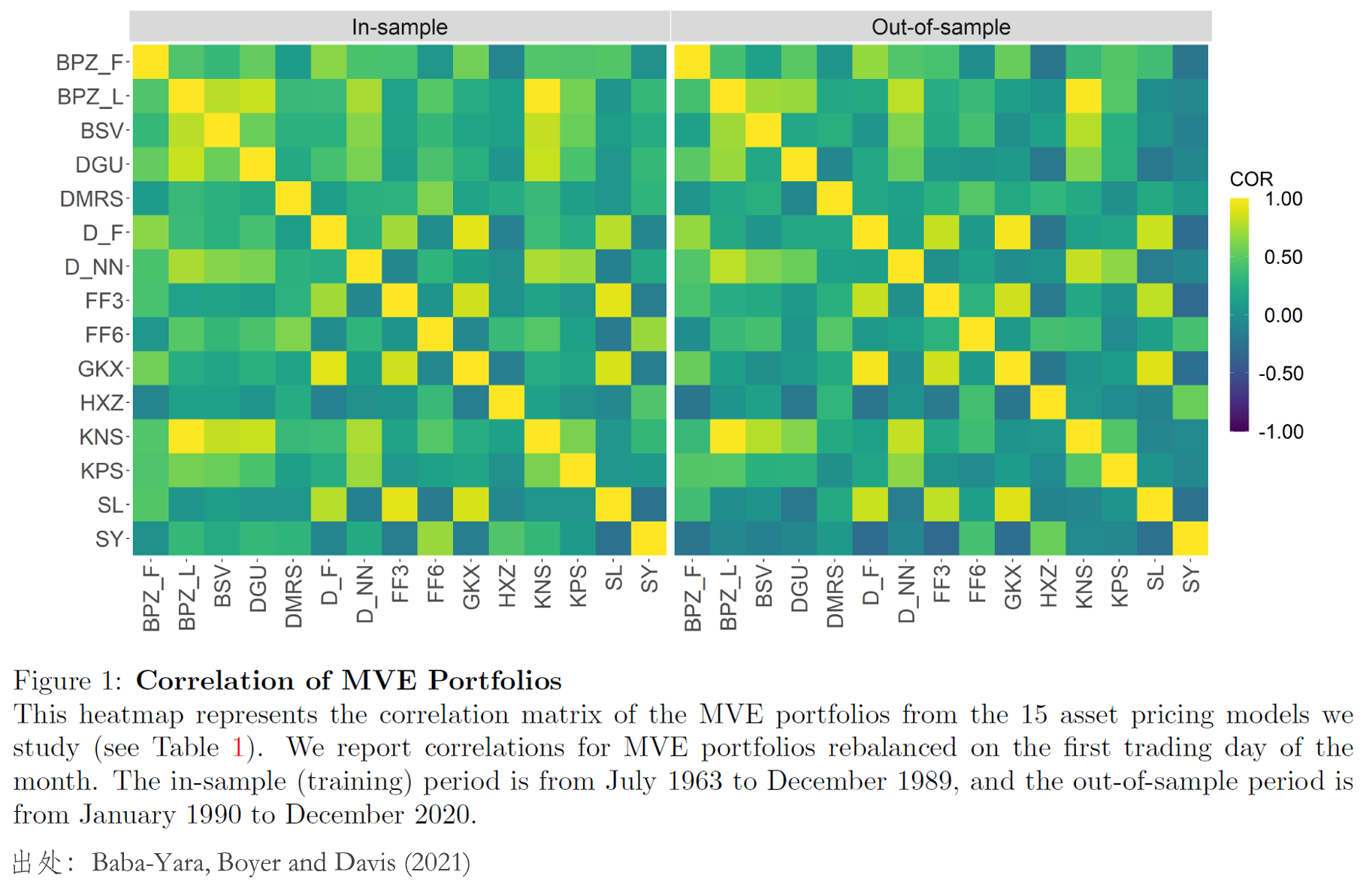
接下(xià)來(lái)看實證結果。該文考察的(de)時(shí)間區(qū)間自 1963 到 2020,爲了(le)在樣本外比較上述模型,該文樣本内區(qū)間截止 Dec 1989;之後爲樣本外。下(xià)圖展示了(le)這(zhè)些模型各自的(de) MVE 組合在樣本内和(hé)樣本外的(de)相關系數。無論是樣本内還(hái)是樣本外,絕大(dà)多(duō)數 MVE 組合似乎都頗爲不同(此處爲本文第四節的(de)討(tǎo)論埋個(gè)伏筆)。
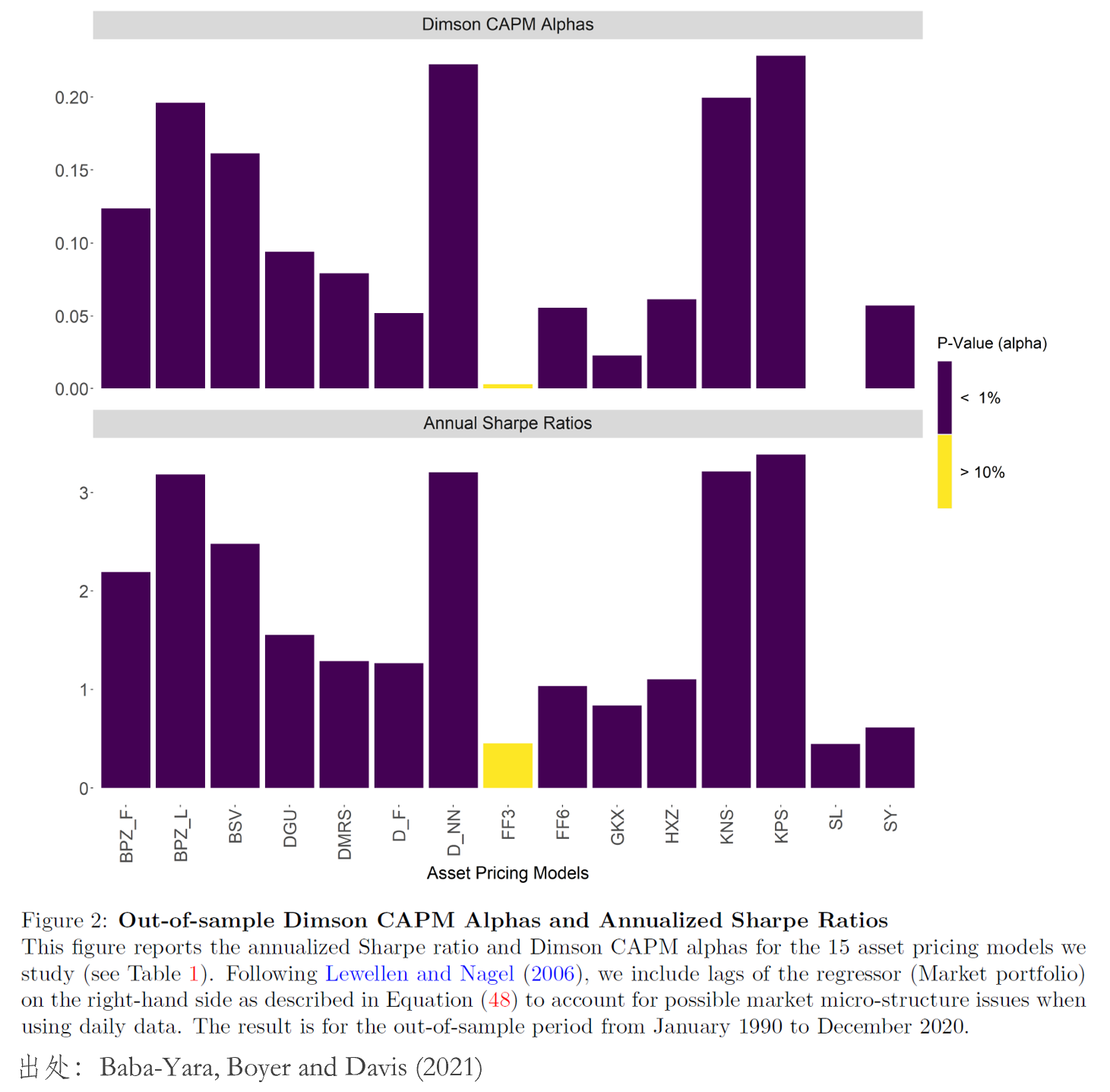
此外,再來(lái)看看這(zhè)些 MVE 組合在樣本外的(de) CAPM-α 以及年化(huà)夏普比率。不出意外,基于機器學習(xí)方法、擁抱協變量高(gāo)維數的(de)新模型在樣本外的(de)風險收益特征均優于傳統模型。在我看來(lái),這(zhè)個(gè)結果對(duì)業界有很大(dà)的(de)意義:(1)雖然在本文一開始,我劇透了(le) factor model failure 這(zhè)個(gè)結論,但是對(duì)業界而言關注的(de)是最大(dà)化(huà)樣本外投資組合的(de)風險收益特征,因此這(zhè)個(gè)結果表明(míng)在協變量的(de)高(gāo)維數時(shí)代,機器學習(xí)方法(如果用(yòng)對(duì)的(de)話(huà))大(dà)有可(kě)爲;(2)傳統強加 ad-hoc 稀疏性假設的(de)模型(比如 FF3、FF6)所代表的(de)投資機會非常弱(體現在很低的(de) CAPM-α 以及年化(huà)夏普比率),所以對(duì)未來(lái)任何以它們爲基準的(de)顯著實證結果都無需太興奮。
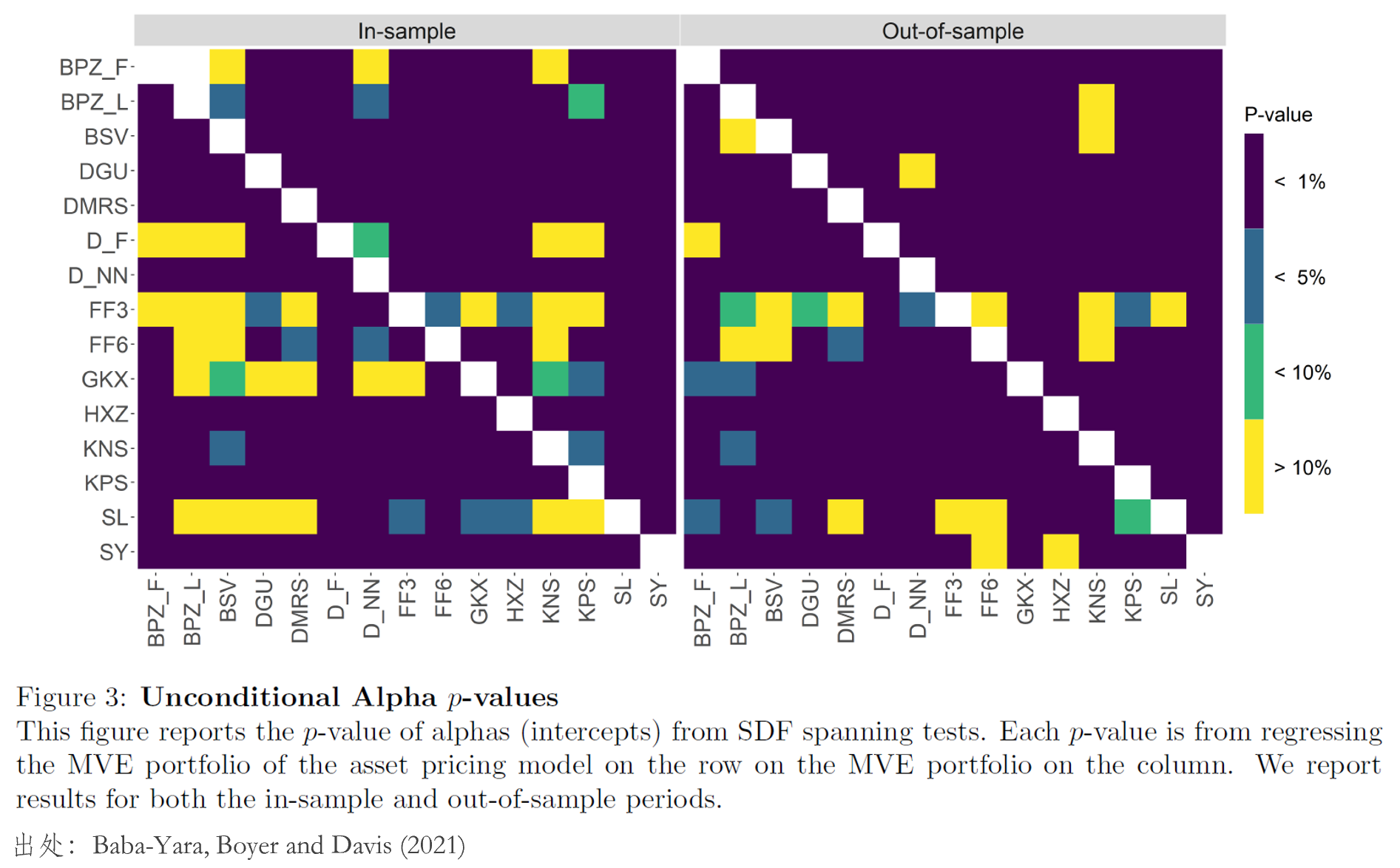
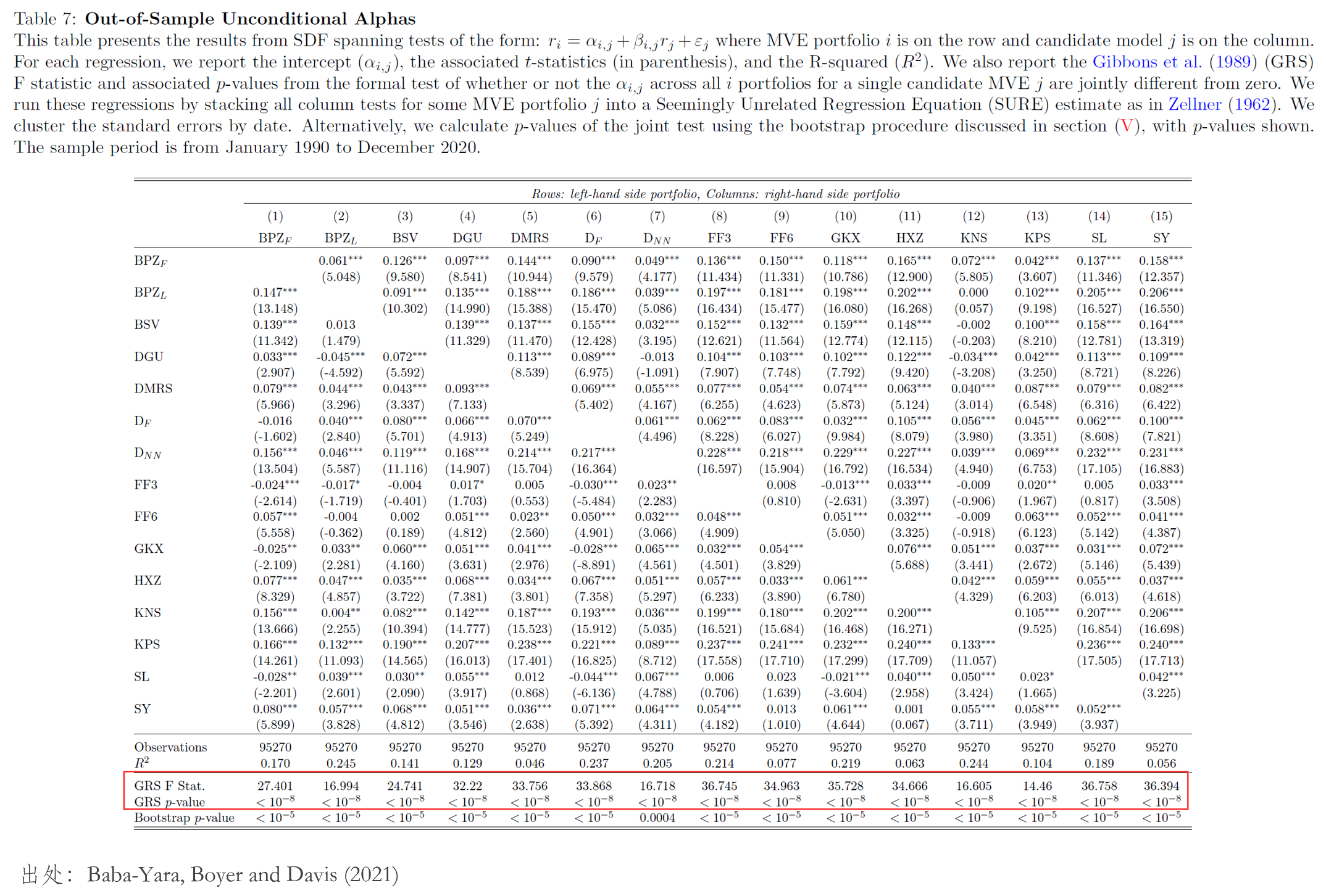
預熱(rè)得(de)差不多(duō)了(le),下(xià)面我們來(lái)看 Baba-Yara, Boyer and Davis (2021) 的(de) main results —— 是否有哪個(gè)模型的(de) MVE 組合能給其他(tā) MVE 組合定價。爲此,該文同時(shí)考察了(le)無條件模型以及條件模型(即
因此,如果有某個(gè)模型是“最優”的(de)話(huà),那麽我們應該能夠看到某一列的(de)顔色都是淺色。然而,事與願違,以樣本外爲例,放眼望去是一片深紫色,說明(míng)哪怕以機器學習(xí)方法構造的(de)模型,也(yě)沒有哪個(gè)能爲所有其他(tā)模型定價。進一步通(tōng)過 GRS test 聯合檢驗每個(gè)基準下(xià)的(de) pricing errors,對(duì)應的(de) F-statistic 都非常大(dà),說明(míng)這(zhè)些 pricing errors 不爲零。
以上結果說明(míng),實證層面,盡管近年來(lái)新的(de)模型層出不窮,但依然沒有所謂的(de)“最優”模型。面對(duì)這(zhè)樣的(de)結果,人(rén)們不禁要問:爲什(shén)麽?
4
實證方面細緻的(de)工作無疑是 Baba-Yara, Boyer and Davis (2021) 一文的(de)重要貢獻,然而關于理(lǐ)論模型的(de)討(tǎo)論才是該文畫(huà)龍點睛的(de)一筆。
由前文論述可(kě)知,站在 MVE 投資組合的(de)視角,一個(gè)多(duō)因子模型可(kě)以被視爲一個(gè)以因子爲标的(de)構造的(de) MVE 組合的(de)權重向量。從理(lǐ)論上說,用(yòng)于構造真實 MVE 組合的(de)因子可(kě)能會有很多(duō),而所有給定的(de)多(duō)因子模型都帶有某種程度的(de)降維處理(lǐ)。比如,最簡單的(de) FF3 使用(yòng)市值和(hé) Book-to-Market Ratio 構造因子。這(zhè)意味著(zhe)該模型認爲這(zhè)兩個(gè)組合在 MVE 組合中的(de)權重非零,而其他(tā)潛在因子的(de)權重都爲零(假設不考慮市場(chǎng)因子)。類似的(de),其他(tā)傳統模型則是人(rén)爲地選擇了(le)盈利、投資、動量等因子,并認爲它們的(de) MVE 權重不爲零;而機器學習(xí)方法則更多(duō)的(de)通(tōng)過數據驅動的(de)方式來(lái)選擇 firm characteristics(以及它們的(de)交互作用(yòng))、構造因子,并決定因子在 MVE 組合中的(de)權重。
在這(zhè)個(gè)視角下(xià),不同的(de)多(duō)因子模型可(kě)以被理(lǐ)解爲對(duì)真實 MVE 組合中的(de)權重施加了(le)不同的(de)先驗(先驗的(de)差異造成了(le)第三節展示的(de)不同模型的(de) MVE 組合的(de)相關系數并不高(gāo))。沿著(zhe)這(zhè)個(gè)思路,Baba-Yara, Boyer and Davis (2021) 提出了(le)一個(gè)貝葉斯框架的(de)理(lǐ)論模型,并發現當潛在的(de)因子個(gè)數非常大(dà)時(shí),使用(yòng)不同先驗的(de)模型無法爲彼此定價。此外,哪怕某個(gè)模型是真正的(de)模型(即它的(de)先驗是正确的(de)),另外一個(gè)使用(yòng)不同先驗的(de)模型也(yě)注定能夠産生該模型無法解釋的(de)超額收益。這(zhè)就是本文一開始提到的(de) impossibility result。在協變量的(de)高(gāo)維數時(shí)代,不存在“最優”的(de)模型 —— 對(duì)于給定的(de)任意模型,總能找到能夠獲得(de)其無法解釋的(de)超額收益的(de)新模型。
In other words, it is impossible to establish a dominant or best asset pricing model in a high dimensional world. Any model that claims dominance can invariably be dominated by a new model with a slight tweak.
—— Baba-Yara, Boyer and Davis (2021)
近年來(lái),factor (model) war 愈演愈烈。而 Baba-Yara, Boyer and Davis (2021) 一文的(de)實證結果和(hé)理(lǐ)論模型無疑給人(rén)們帶來(lái)了(le)全新的(de)思考。至少對(duì)我來(lái)說,再看傳統模型在那裏 PK 來(lái) PK 去實在是不痛不癢。對(duì)于業界實務來(lái)說,人(rén)們使用(yòng)多(duō)因子模型降維是爲了(le)減少估計誤差對(duì) MVE 組合權重的(de)影(yǐng)響。因此,回答(dá)更關鍵的(de)問題,即應該使用(yòng)何種的(de)先驗(回想一下(xià)《稀疏性幻覺》)以及如何更合理(lǐ)的(de)使用(yòng)機器學習(xí)方法構造因子以及計算(suàn)它們的(de) MVE 權重,這(zhè)些才是有價值的(de)研究。
期待 Baba-Yara, Boyer and Davis (2021) 早日見刊。
參考文獻
Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.
Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.
Chen, L., M. Pelger, and J. Zhu (2019). Deep learning in asset pricing. Working paper.
Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton, NJ: Princeton University Press.
Daniel, K., L. Mota, S. Rottke, and T. Santos (2020). The cross-section of risk and returns. Review of Financial Studies 33(5), 1927 – 1979.
Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.
Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.
Gu, S., B. T. Kelly, and D. Xiu (2021). Autoencoder asset pricing models. Journal of Econometrics 222(1), 429 – 450.
Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.
Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.
Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
Roll, R. (1977). A critique of the asset pricing theory’s tests Part I: On past and potential testability of the theory. Journal of Financial Economics 4(2), 129 – 176.
Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。