因子動量與動量因子

發布時(shí)間：2023-02-15 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：Ehsani and Linnainmaa (2022) 是 post Fama-French 時(shí)代一篇難得(de)的(de)實證佳作。

很久沒有介紹實證研究了(le)。因爲即便是大(dà)佬在另類數據的(de)加持下(xià)發表在 top 3 上的(de)那些，也(yě)并無太多(duō)驚豔。但今天是個(gè)例外，我想深度解讀 Ehsani and Linnainmaa (2022)，并利用(yòng) A 股數據做(zuò)一些相似的(de)實證。Ehsani and Linnainmaa (2022) 研究的(de)是一個(gè)純粹且重要的(de)問題：截面動量（momentum）。更确切地說，該文研究了(le)因子動量和(hé)（個(gè)股的(de)）動量因子之間的(de)關聯。在我看來(lái)，這(zhè)篇文章(zhāng)是 post Fama-French 時(shí)代一篇難得(de)的(de)實證佳作。這(zhè)一點從它能被發表在 Journal of Finance 上就足以說明(míng)。在剛剛結束的(de) AFA 2023 年會上，該文被評爲 2022 DFA Distinguished Paper。

如同是 Fama-French 多(duō)因子模型的(de)“心結”一樣，個(gè)股上的(de)截面動量（即 Carhart 1997 發現的(de) UMD 因子）也(yě)是實證資産定價繞不過去的(de)坎兒(ér)。其在實證資産定價中的(de)特殊地位可(kě)以由下(xià)面這(zhè)句話(huà)精彩地概括：不包含動量因子的(de)多(duō)因子模型無法解釋動量因子，而加入動量因子後，模型解釋力的(de)提升也(yě)僅僅體現在能夠解釋動量因子（Fama and French 2016）。

面對(duì)無處不在的(de)動量（Asness, Moskowitz and Pedersen 2013），Ehsani and Linnainmaa (2022) 以因子動量（factor momentum）爲切入點，針對(duì)因子動量和(hé)個(gè)股動量，回答(dá)了(le)以下(xià)問題：

問題一：因子收益率在時(shí)序上是否有自相關性？

問題二：因子滿足何種條件時(shí)，更容易出現自相關性？

問題三：利用(yòng)自相關性、基于因子曆史收益率構造的(de)因子動量策略（注意，它類似于 UMD，是以因子組合爲 assets 的(de)截面動量策略）和(hé)個(gè)股截面動量因子（即 UMD）有什(shén)麽關系？誰是因？誰又是果？

問題四：因子動量能否解釋個(gè)股殘差動量？

問題五：如何理(lǐ)解 UMD 因子和(hé)其他(tā)因子時(shí)序無關的(de)實證現象？

下(xià)面就通(tōng)過 5 個(gè)小節介紹 Ehsani and Linnainmaa (2022) 在上述五個(gè)問題中的(de)實證結果。此外，在問題一、三以及五中會輔以基于 A 股的(de)實證。數據來(lái)自 BetaPlus 小組。

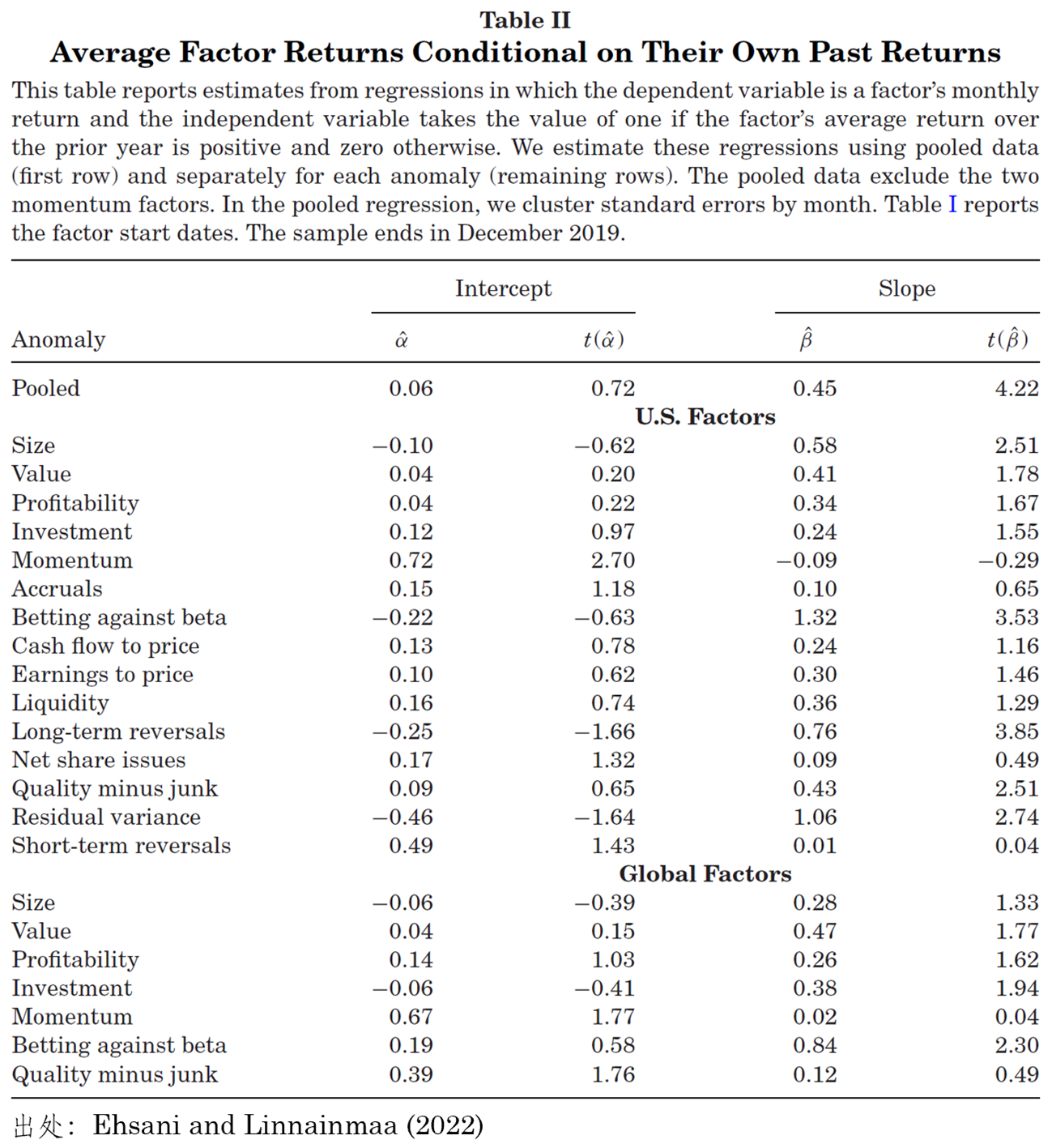
因子收益率存在時(shí)序自相關性是之後以因子爲 assets 構造因子動量的(de)基礎，且自相關性應普遍存在于常見的(de)因子之中，否則故意挑那些“好使”的(de)因子來(lái)構造就有 data snooping 問題。爲此，在實證的(de)一開始，Ehsani and Linnainmaa (2022) 考察了(le)美(měi)股以及全球市場(chǎng)中常見因子收益率的(de)自相關性。他(tā)們以過去 12 個(gè)月(yuè)的(de)曆史收益率的(de)正負構造了(le)自變量：當收益率爲正時(shí)，自變量取值爲 1，反之爲 0。

在時(shí)序回歸中，用(yòng)下(xià)個(gè)月(yuè)的(de)收益率對(duì)當月(yuè)的(de)自變量進行回歸（且包含截距項）。在該回歸模型中，截距項代表了(le)過去 12 個(gè)月(yuè)的(de)曆史收益率爲負時(shí)，下(xià)個(gè)月(yuè)的(de)條件月(yuè)均收益率；而自變量的(de)回歸系數則表示當過去 12 個(gè)月(yuè)的(de)曆史收益率爲正 vs. 過去 12 個(gè)月(yuè)曆史收益率爲負時(shí)，下(xià)個(gè)月(yuè)條件月(yuè)均收益率的(de)差值。由下(xià)表中的(de)結果（以美(měi)股中的(de)因子爲例）可(kě)知，除了(le)動量外，其他(tā)常見因子自變量的(de)回歸系數均爲正，且絕大(dà)多(duō)數在 5% 或 10% 的(de)顯著性水(shuǐ)平下(xià)顯著，說明(míng)因子收益率的(de)自相關性是普遍存在的(de)，這(zhè)爲後面構造因子動量奠定了(le)基礎。

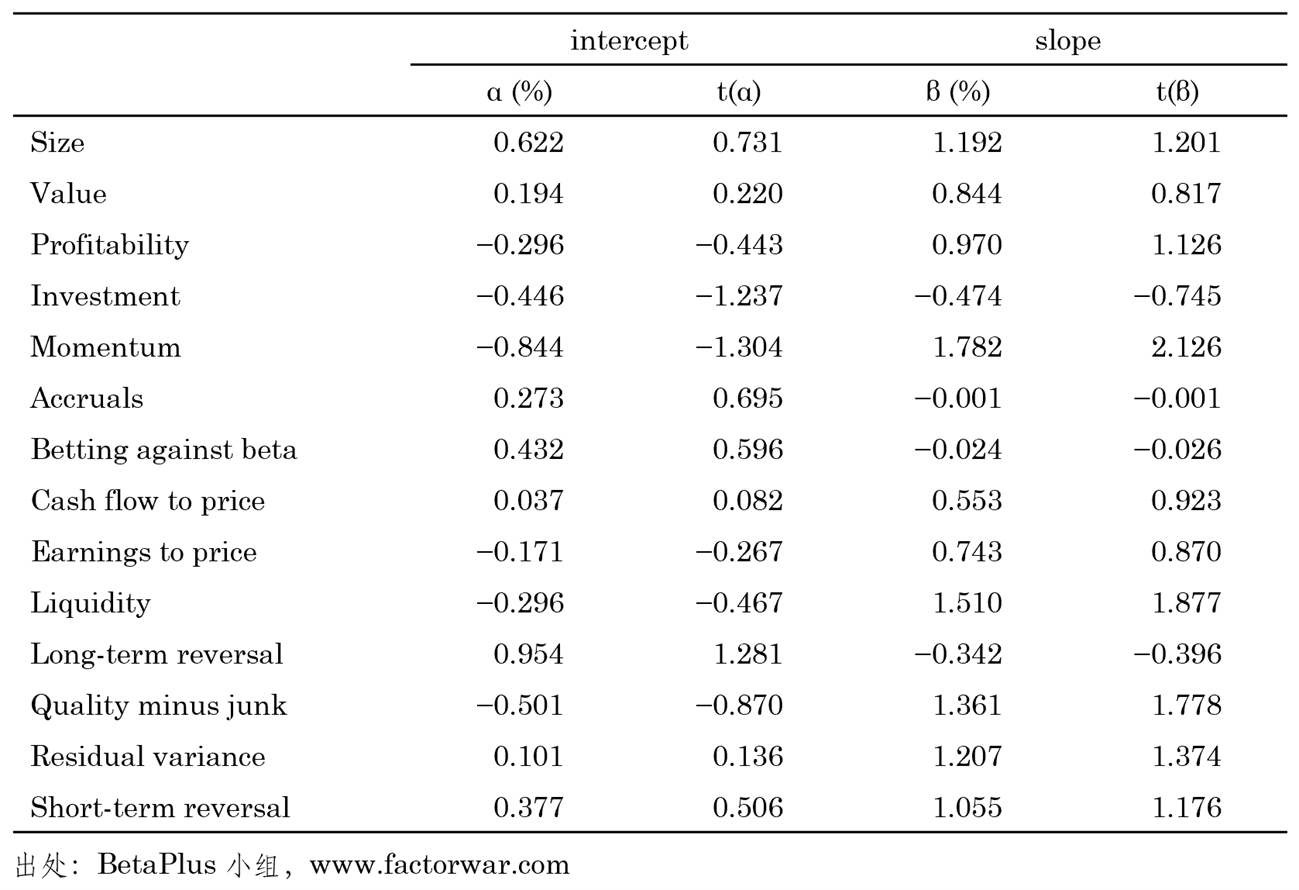
類似的(de)，來(lái)看一下(xià) A 股的(de)實證結果。BetaPlus 小組依上表構造了(le)除 Net share issues 之外的(de)其他(tā)因子（共 14 個(gè)），實證區(qū)間爲 2000 年 1 月(yuè)到 2023 年 1 月(yuè)。由于計算(suàn)曆史收益率需要用(yòng)掉 12 期數據，因此以下(xià)回歸結果是基于 2001 年 1 月(yuè)到 2023 年 1 月(yuè)的(de)數據（本文其他(tā) A 股實證結果的(de)實證區(qū)間類似）。

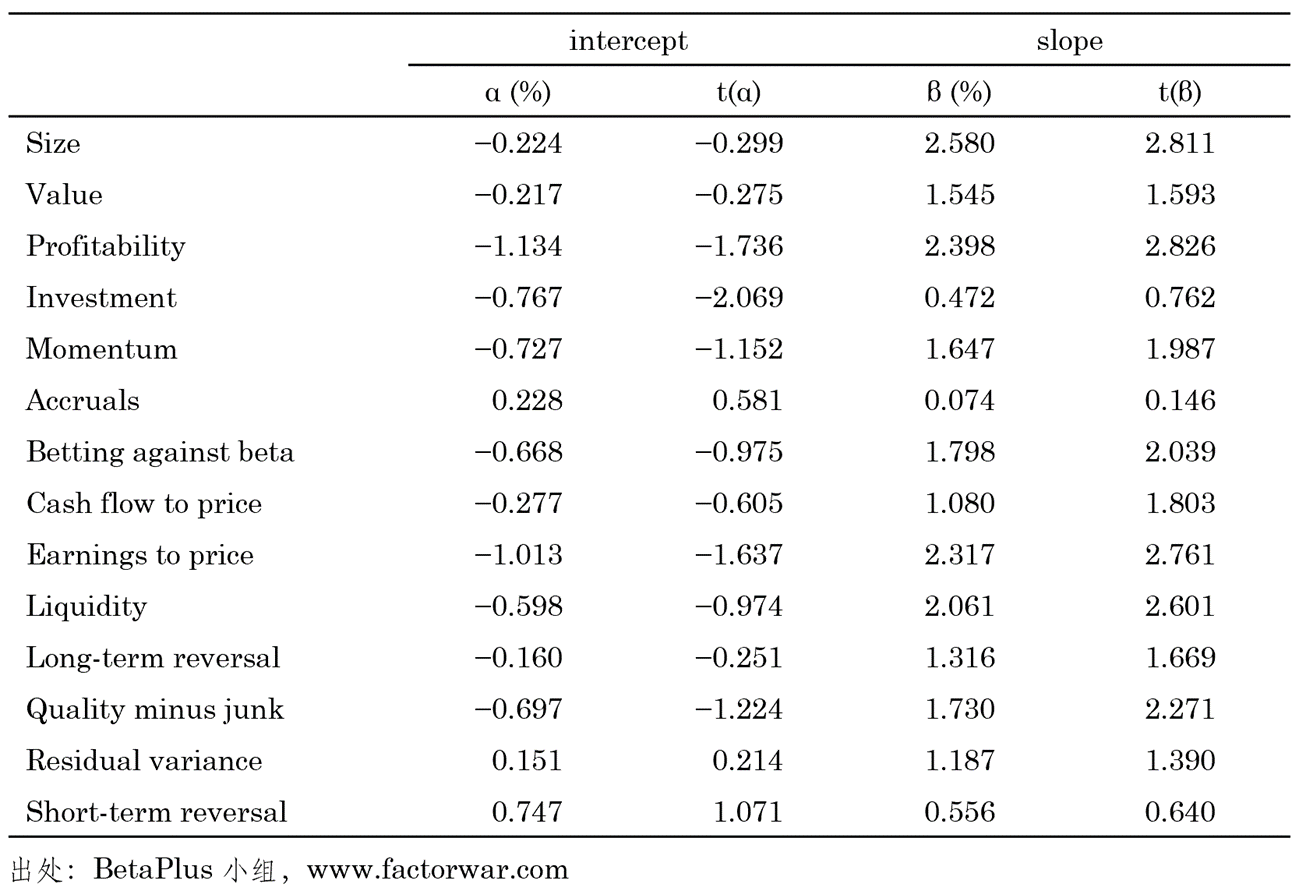
從上述結果來(lái)看，基于 A 股的(de)結果和(hé)基于美(měi)股的(de)并不是那麽一緻。這(zhè)體現在并非絕大(dà)多(duō)數因子自變量的(de)回歸系數顯著爲正。考慮到中美(měi)兩個(gè)市場(chǎng)的(de)差異以及個(gè)股動量效應在 A 股長(cháng)期來(lái)看并不顯著這(zhè)樣一個(gè)經驗事實，上述結果并不意外。不過頗有意思的(de)是，如果将定義自變量的(de)曆史收益率換成過去 7 至 12 個(gè)月(yuè)的(de)累計收益率（而非 1 到 12 個(gè)月(yuè)），則回歸結果（下(xià)表）反而更加貼近美(měi)股。

上述實證結果背後的(de)含義不在本文的(de)討(tǎo)論範圍之内。但是在下(xià)文針對(duì) A 股的(de)實證中，會同時(shí)慮兩個(gè)版本（即基于過去 12 個(gè)月(yuè)收益率構造的(de)因子動量，以及基于過去 7 – 12 個(gè)月(yuè)收益率構造的(de)因子動量）。

接下(xià)來(lái)，Ehsani and Linnainmaa (2022) 基于 Kozak, Nagel and Santosh (2018) 的(de)由情緒驅動的(de)投資者理(lǐ)論模型討(tǎo)論了(le)因子收益率存在時(shí)序自相關性的(de)原因。具體的(de)推導，感興趣的(de)小夥伴請參考論文原文，這(zhè)裏直接說結論：

1. 投資者情緒存在很強的(de)持續性，因而造成了(le)因子收益率的(de)自相關性；

2. 越是那些和(hé)股票(piào)協方差矩陣關系密切的(de)因子，即更能解釋資産收益率共同運動的(de)因子，其收益率的(de)自相關性越強。

上述結論和(hé) Kozak, Nagel and Santosh (2018) 利用(yòng)“市場(chǎng)中不應持續存在近似無風險的(de)套利機會”這(zhè)個(gè)假設對(duì)多(duō)因子模型給出的(de)啓示相同：雖然市場(chǎng)中存在套利者，但是出于對(duì)系統性風險的(de)規避，他(tā)們不會對(duì)那些能夠解釋資産共同運動的(de)因子充分(fēn)套利，從而留下(xià)了(le)收益率的(de)自相關性。上述理(lǐ)論模型對(duì)于實證的(de)啓示是，當基于個(gè)股收益率的(de)協方差矩陣、通(tōng)過 PCA 構造隐性因子（即主成分(fēn)因子）時(shí)，利用(yòng)高(gāo)特征值（即波動更大(dà)）的(de)那些隐性因子所構造的(de)因子動量要比基于低特征值（即波動更低，從而更有可(kě)能被充分(fēn)套利）的(de)隐性因子的(de)因子動量要顯著。

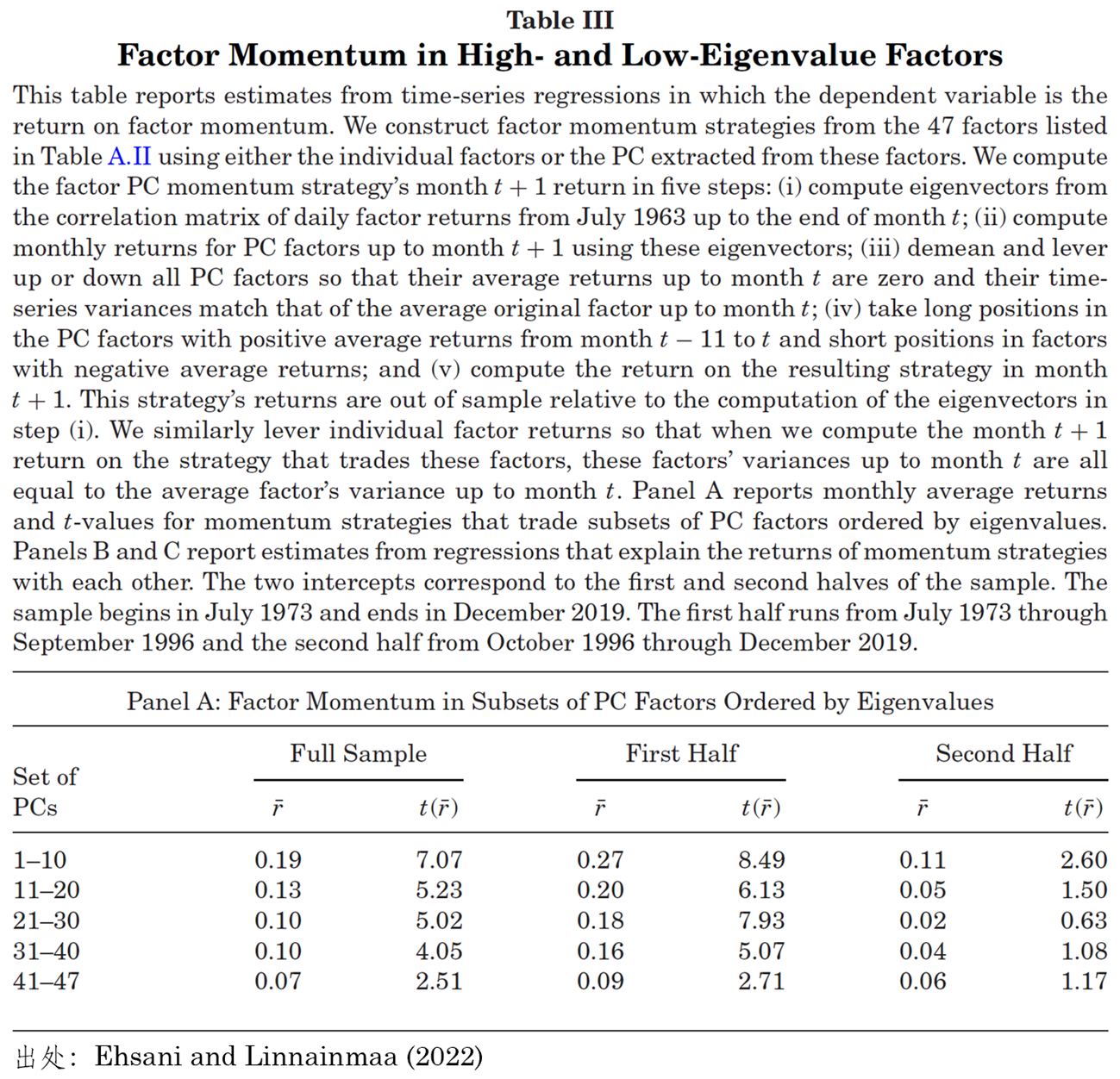
爲了(le)驗證這(zhè)一點，Ehsani and Linnainmaa (2022) 使用(yòng)了(le) Kozak, Nagel and Santosh (2020) 一文中涉及的(de) 47 個(gè)風格因子，并通(tōng)過 PCA 将它們轉化(huà)爲 47 個(gè)主成分(fēn)，并按照(zhào)其對(duì)應特征值從高(gāo)到底分(fēn)成五組：（1）PC1 – PC10；（2）PC11 – PC20；（3）PC21 – PC30；（4）PC31 – PC40；以及（5）PC41 – PC47。通(tōng)過使用(yòng)五組分(fēn)别構造因子動量，Ehsani and Linnainmaa (2022) 證實了(le)理(lǐ)論模型的(de)推論。

以原文 Table III Panel A 爲例（上表），它彙報了(le)整個(gè)實證區(qū)間以及前後各半個(gè)實證區(qū)間内，通(tōng)過上述五組主成分(fēn)組合構造的(de)因子動量策略的(de)月(yuè)均收益率及其 t-statistics。以 PC1 – PC10（即特征值最大(dà)的(de) 10 個(gè)主成分(fēn)）爲例，在構造因子動量時(shí)，在 t 期，根據這(zhè) 10 個(gè)組合過去 12 個(gè)月(yuè)份收益率的(de)正負爲依據，做(zuò)多(duō)收益率爲正的(de) PCs 并做(zuò)空收益率爲負的(de) PCs，以此構造因子動量的(de)多(duō)空組合。在 full sample 中，該因子動量組合月(yuè)均收益率 t-statistics 高(gāo)達 7.07；這(zhè)個(gè)數值在前後各半個(gè)實證區(qū)間内變爲 8.49 和(hé) 2.60（a side note：即便是因子動量，也(yě)無法逃脫因更多(duō)研究被發表以及被更多(duō)人(rén)來(lái)交易而逐漸變弱這(zhè)樣一個(gè)事實）。

上述結果顯示，無論在哪個(gè)實證窗(chuāng)口内，基于更高(gāo)特征值的(de)主成分(fēn)因子所構造的(de)因子動量都相對(duì)來(lái)說更加顯著（經濟上和(hé)統計上均如此）。此外，該表的(de) Panels B 和(hé) C 比較了(le)高(gāo)特征值和(hé)低特征值構造的(de)因子動量相互檢驗的(de)結果，結果顯示前者的(de)因子動量無法被後者解釋。

實證的(de)第三部分(fēn)研究的(de)是人(rén)們最關心的(de)因子動量和(hé)個(gè)股上的(de)動量因子之間的(de)關系。

由 APT 可(kě)知，個(gè)股收益率在理(lǐ)論上可(kě)以分(fēn)解爲因子收益率的(de)線性組合。以此爲基礎， Ehsani and Linnainmaa (2022) 通(tōng)過數學推導将個(gè)股動量的(de)預期收益率拆解成爲四個(gè)部分(fēn)，其中第一部分(fēn)（也(yě)是最重要的(de)一部分(fēn)）正是由因子收益率的(de)時(shí)序自相關性的(de)高(gāo)低決定。

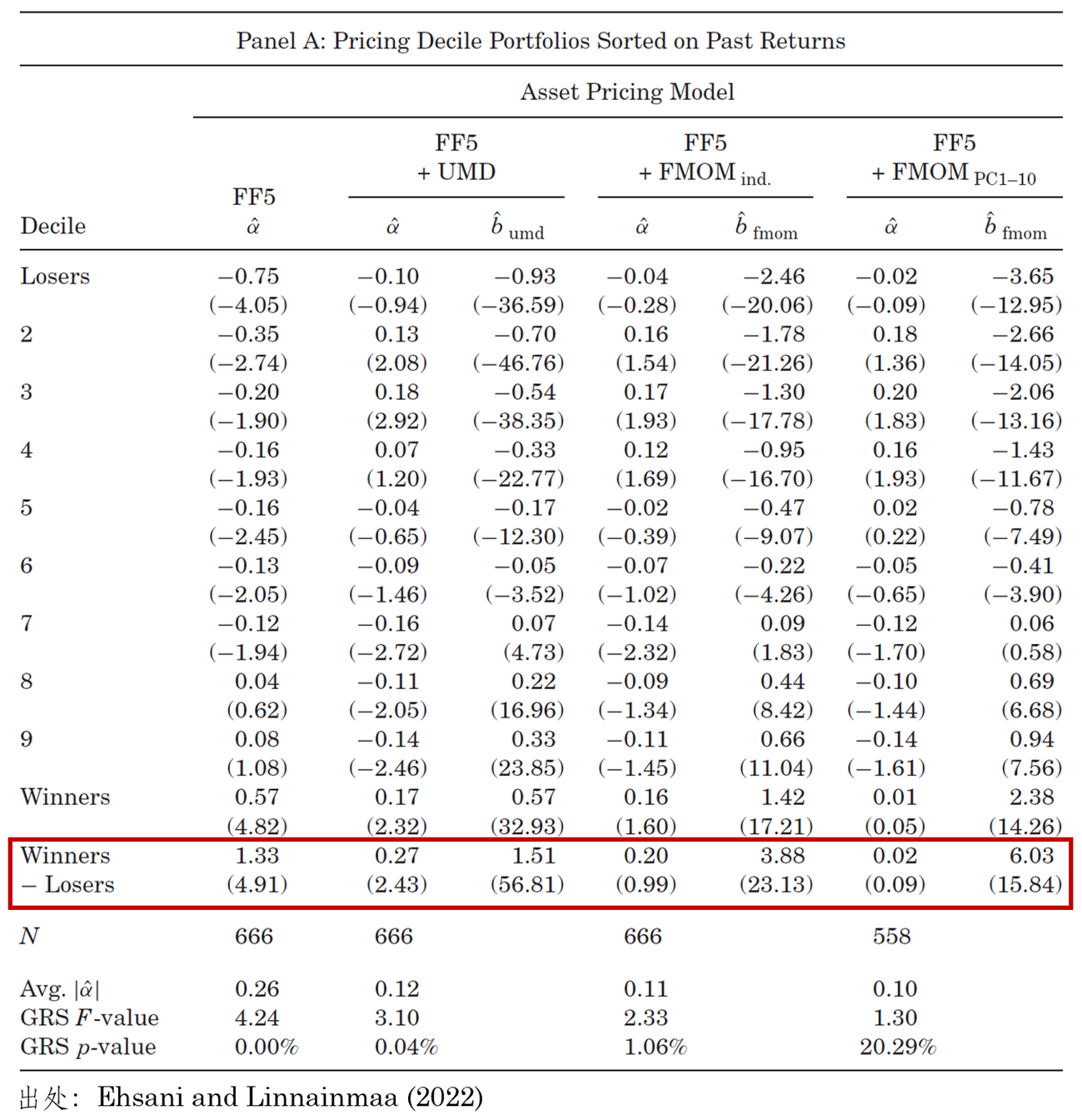
上述拆解表明(míng)，因子動量（部分(fēn)甚至很大(dà)部分(fēn)）驅動了(le)個(gè)股的(de)動量因子。因此，實證上可(kě)以預期加入因子動量的(de)多(duō)因子模型能夠解釋個(gè)股動量。實證結果如下(xià)表所示。在實證中，作爲被檢驗資産的(de)除了(le)個(gè)股動量（表中 Winners – Losers 之外，還(hái)有根據該變量排序構造的(de) 10 個(gè) sorted portfolios）；作爲多(duō)因子模型的(de)包括 FF5，FF5 + UMD 因子（對(duì)，你沒看錯，在 FF5 中加上 UMD 因子隻爲了(le)額外解釋個(gè)股動量）；FF5 + 基于常見因子的(de)因子動量（FF5 + $\mbox{FMOM}_{ind}$ ）以及 FF5 + 基于前 10 個(gè)主成分(fēn)因子的(de)因子動量（FF5 + $\mbox{FMOM}_{PC1-10}$ ）。

作爲解讀，讓我們關注 Winners – Losers 這(zhè)一行。其 FF5-α 的(de) t-statistic 爲 4.91（顯然 FF5 對(duì)個(gè)股動量無能爲力）。當把 UMD 因子加入 FF5 之後，t-statistics 降爲 2.43（依然存在 α 應是由于回歸方程左側個(gè)股動量和(hé)右側 UMD 因子構造方式不完全一緻所緻）。最後，當把因子動量（無論是基于常見因子，還(hái)是基于主成分(fēn)因子）加入 FF5 之後，個(gè)股動量均無法獲得(de)顯著的(de)超額收益。當使用(yòng)常見因子時(shí)，其超額收益的(de) t-statistic 爲 0.99；而當使用(yòng)主成分(fēn)因子時(shí)，其 t-statistic 僅爲 0.09。上述結果表明(míng)，因子動量能夠解釋個(gè)股動量。

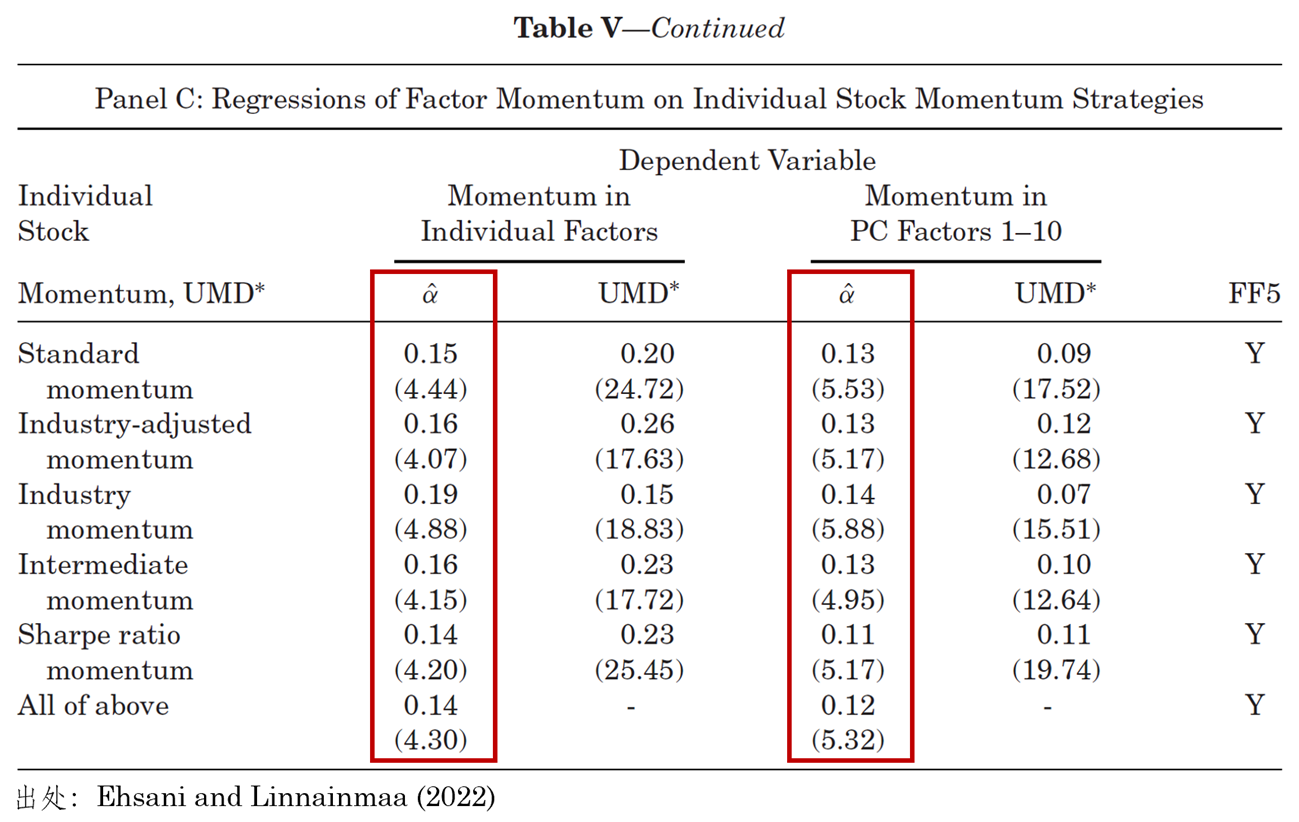
那麽反過來(lái)，加入了(le)個(gè)股動量 UMD 因子的(de)多(duō)因子模型能否解釋因子動量呢(ne)？下(xià)表給出了(le)解答(dá)。請注意，在以下(xià)實證中，兩位作者除了(le)标準的(de) UMD 因子（表中記爲 Standard momentum）外，還(hái)考察了(le)各種版本的(de)花式 UMD 因子（例如 Industry-adjusted momentum 是經過行業收益率調整之後的(de) UMD，等）。然而，無論使用(yòng)哪個(gè)版本的(de) UMD（甚至是全部版本一起上），其和(hé) FF5 一起構造的(de)多(duō)因子模型均無法解釋因子動量（考察标出來(lái)的(de)兩列 α）。當使用(yòng)常見因子構造因子動量時(shí)，其超額收益的(de) t-statistic 在不同版本模型下(xià)均在 4.0 以上；而當使用(yòng)主成分(fēn)因子構造因子動量時(shí)，除中期動量版本的(de) UMD 外，因子動量超額收益 t-statistic 在其他(tā)模型下(xià)均在 5.0 以上。因此，個(gè)股動量無法解釋因子動量。

下(xià)面來(lái)看看 A 股的(de)結果。回顧第一節，我們針對(duì) A 股構造了(le)常見的(de) 14 個(gè)因子，除去動量本身外，我們使用(yòng)剩餘 13 個(gè)因子構造因子動量（即在每一期，回看過去一段時(shí)間的(de)曆史收益率，然後做(zuò)多(duō)曆史收益率爲正的(de)因子，做(zuò)空曆史收益率爲負的(de)因子，以此構造因子動量）。在本節實證中，以 FF5 爲基礎（FF5 數據來(lái)自 BetaPlus 小組針對(duì) A 股構造并維護的(de)數據，見 www.factorwar.com），先後加上 UMD 因子和(hé)因子動量作爲多(duō)因子模型，即 FF5 +UMD 和(hé) FF5 + Factor Mom。當使用(yòng) FF5 + Factor Mom 作爲多(duō)因子模型時(shí)，考察 UMD 因子能否獲得(de)超額收益。結果顯示，UMD 月(yuè)均超額收益的(de) t-statistic 爲 1.416，并不顯著，和(hé)美(měi)股一緻。不過有意思的(de)是，當使用(yòng) FF5 + UMD 作爲多(duō)因子模型給因子動量定價時(shí)，後者的(de)超額收益的(de) t-statistic 也(yě)僅爲 1.551，也(yě)并不顯著，這(zhè)和(hé)美(měi)股的(de)結果并不一緻。

以上結果是通(tōng)過遵循原文的(de)方式，即使用(yòng)過去 12 個(gè)月(yuè)收益率爲依據構造因子動量。作爲參考，下(xià)面再來(lái)看看如果使用(yòng)過去 7 – 12 個(gè)月(yuè)的(de)收益率爲依據構造因子動量會發生什(shén)麽。在這(zhè)個(gè)設定下(xià)，A 股上呈現出和(hé)美(měi)股一緻的(de)結果：UMD 相對(duì) FF5 + 因子動量的(de)超額收益 t-statistic 僅爲 1.405；而因子動量相對(duì) FF5 + UMD 的(de)超額收益 t-statistic 高(gāo)達 3.304。因此，因子動量能夠解釋個(gè)股動量，反之則不然。

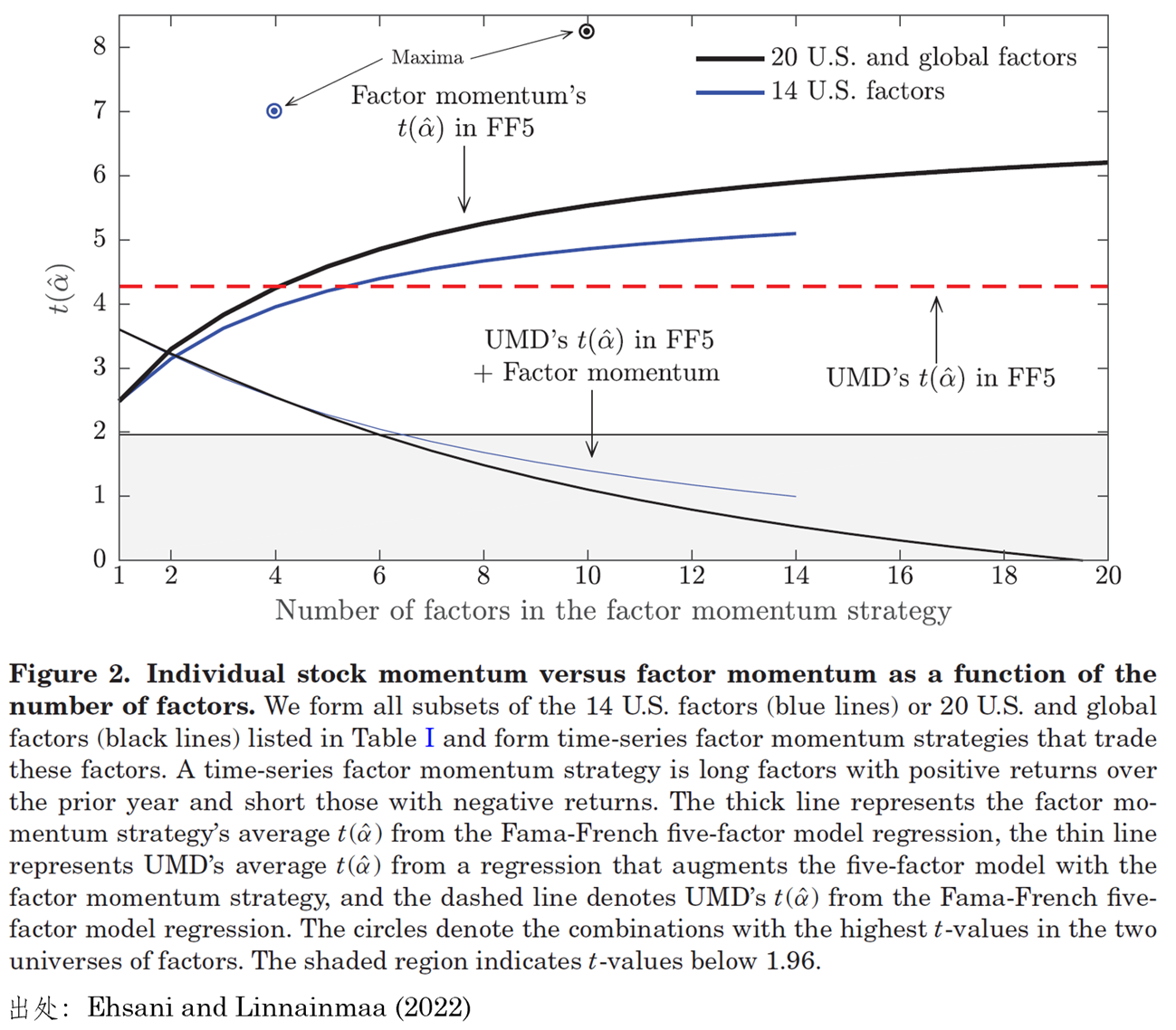
由于本節介紹的(de)内容是 Ehsani and Linnainmaa (2022) 的(de) main results，因此兩位作者也(yě)進行了(le)相當充分(fēn)的(de)穩健性檢驗，其中之一就是因子動量對(duì)具體哪些因子以及因子的(de)個(gè)數是否敏感。以 14 個(gè)美(měi)股因子爲例，該文考察了(le)因子個(gè)數從 1 變化(huà)到 14 的(de)情況（1 就相當于是單因子根據動量擇時(shí)；14 相當于所有因子一起上）；當因子的(de)個(gè)數在 1 到 14 之間時(shí)，他(tā)們則考察了(le)從所有因子中選出目标數目個(gè)因子的(de)全部排列組合，計算(suàn)每個(gè)排列組合構造的(de)因子動量，并将它們的(de)均值作爲該個(gè)數下(xià)的(de)結果。下(xià)圖展示了(le)因子動量相對(duì)于 FF5 的(de)超額收益的(de) t-statistic 如何随因子個(gè)數變化(huà)。從圖中可(kě)以看出，t-statistic 随因子的(de)個(gè)數增加，且持續顯著。

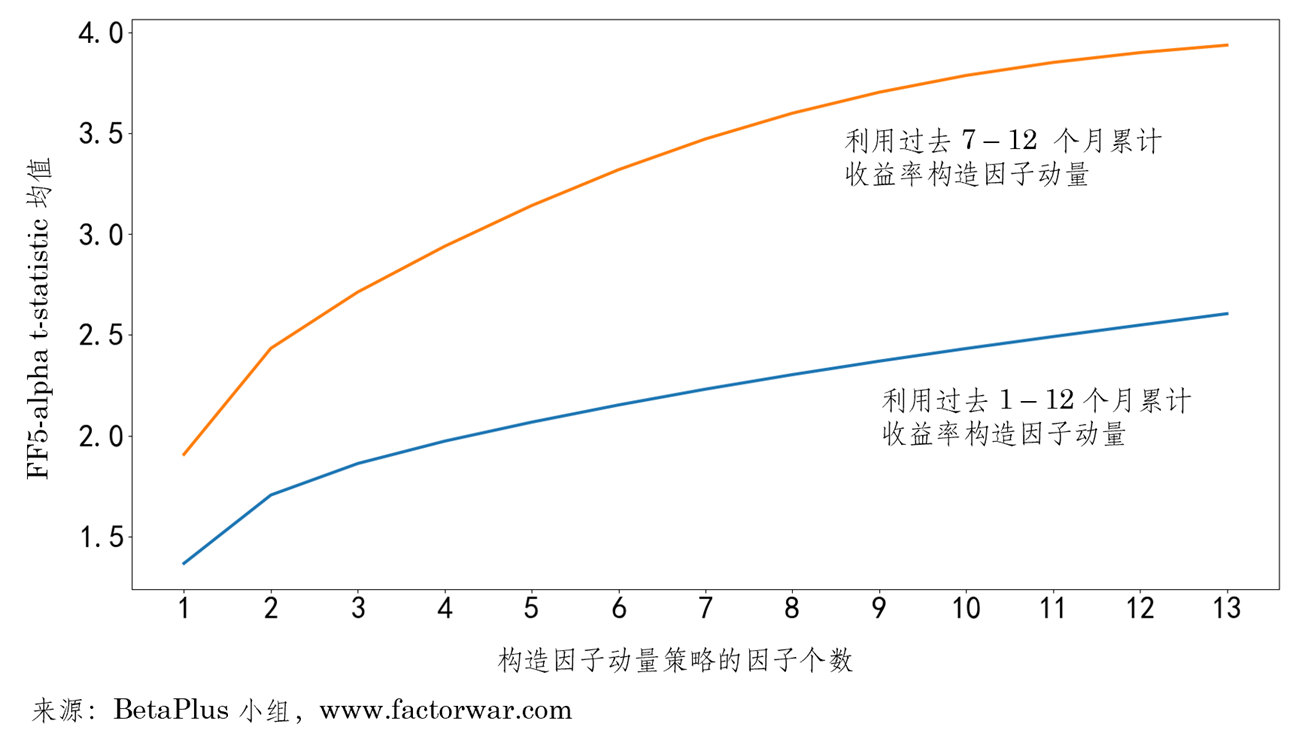
我也(yě)對(duì) A 股進行了(le)同樣的(de)實證。下(xià)圖展示了(le)兩種構造因子動量的(de)方法。當使用(yòng)和(hé)美(měi)股一樣的(de)方法時(shí)（即根據過去 12 個(gè)月(yuè)的(de)收益率），當因子的(de)個(gè)數不少于 4 時(shí)，因子動量就能獲得(de)相對(duì) FF5 的(de)顯著超額收益；而當使用(yòng)過去 7 – 12 個(gè)月(yuè)收益率時(shí)，當因子不少于 2 個(gè)時(shí)，即可(kě)獲得(de)相對(duì) FF5 的(de)顯著超額收益。此外，第二種方法的(de)超額收益持續優于第一種方法。

本節來(lái)看看殘差動量。這(zhè)雖然不是 Ehsani and Linnainmaa (2022) 的(de) main results，但卻是我格外感興趣的(de)一個(gè)内容，因爲我一直對(duì)殘差動量持懷疑态度（見《殘差動量——有理(lǐ)有據還(hái)是數據挖掘》）。Ehsani and Linnainmaa (2022) 的(de)研究表明(míng)，殘差動量是遺漏變量造成的(de)。

爲了(le)從直覺上理(lǐ)解，舉個(gè)最簡單的(de)例子。假設個(gè)股收益率和(hé)兩個(gè)因子有關，而分(fēn)析者隻觀測到其中一個(gè)因子，而把另一個(gè)因子當作特質性收益率的(de)一部分(fēn)。在這(zhè)種情況下(xià)，即便個(gè)股特質性收益率滿足 IID，那個(gè)被遺漏的(de)因子的(de)動量也(yě)會被錯誤地視爲殘差動量。

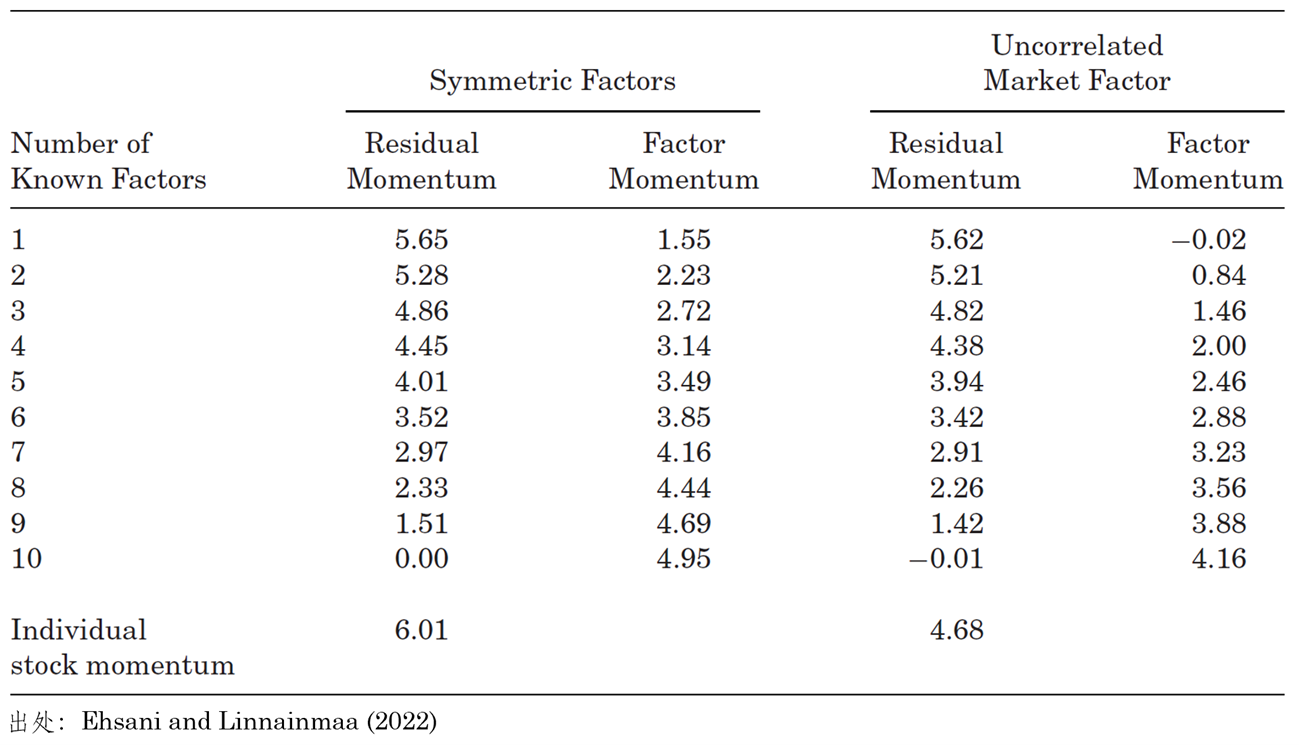
Ehsani and Linnainmaa (2022) 通(tōng)過模拟和(hé)實際數據證實了(le)上述猜想。在模拟中，他(tā)們假設資産收益率由 10 個(gè)因子決定，并考慮了(le)兩個(gè)情景：（1）10 個(gè)因子的(de)自相關性相似，且對(duì)資産收益率波動的(de)解釋大(dà)小也(yě)相似；（2）10 個(gè)因子中第一個(gè)因子解釋資産的(de)波動是其他(tā)每個(gè)因子的(de) 5 倍，且第一個(gè)因子的(de)收益率在時(shí)序上是不相關的(de)（所以第一個(gè)因子可(kě)以理(lǐ)解爲市場(chǎng)因子）。在每個(gè)情境中，他(tā)們分(fēn)别考慮已知 N 個(gè)因子（N 取值 1 到 10）的(de)情況，隻要 N < 10，就說明(míng)計算(suàn)殘差動量時(shí)遺漏了(le) 10 – N 個(gè)因子。

下(xià)表展示了(le)模拟的(de)結果，其中 Symmetric Factors 表示情景一；Uncorrelated Market Factor 表示情景二。以情景一爲例，在計算(suàn)殘差動量時(shí)，遺漏的(de)變量越多(duō)（即 Number of Known Factors 越小），殘差動量的(de) t-statistic 則越大(dà)。當模型不存在遺漏變量時(shí)，殘差動量也(yě)随之消失。此外，表中另一個(gè)非常重要的(de)結果是，在情景二中，個(gè)股動量的(de) t-statistic 爲 4.68（表格最下(xià)方），而當把市場(chǎng)因子剔除後計算(suàn)殘差動量時(shí)，其 t-statistic 則上升到 5.62（表格第一行）。這(zhè)是因爲，當剔除掉這(zhè)個(gè)沒有自相關的(de)市場(chǎng)因子後，資産收益率的(de)剩餘部分(fēn)更好地捕捉了(le)被遺漏的(de)那 9 個(gè)因子的(de)自相關性，從而造成殘差動量相比于包含市場(chǎng)因子計算(suàn)的(de)個(gè)股動量更加顯著。

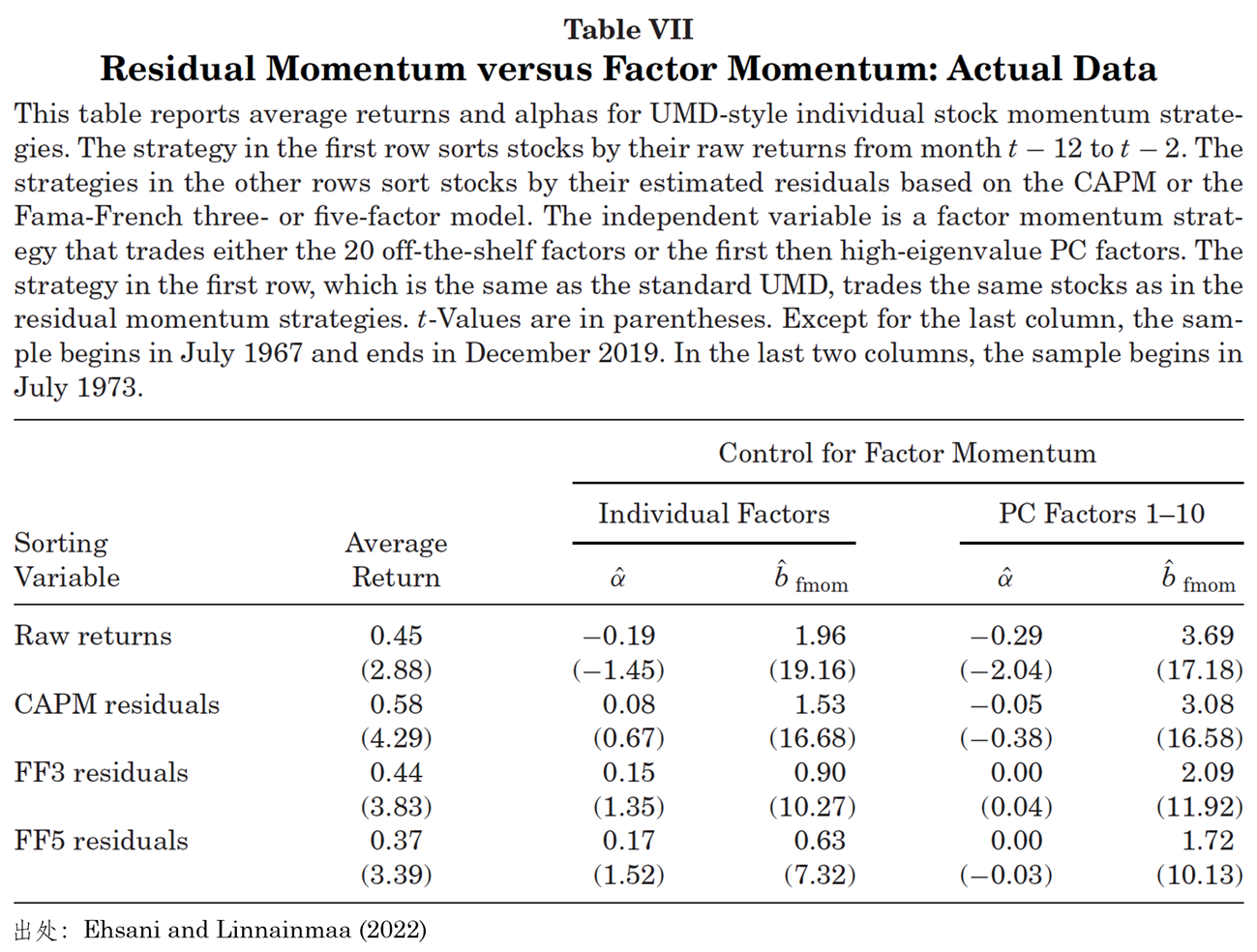
基于實際數據的(de)實證結果又如何呢(ne)？下(xià)表中分(fēn)别考察了(le)原始的(de) UMD 以及基于 CAPM、FF3 和(hé) FF5 計算(suàn)的(de)殘差動量。觀察 Average Return 那一列，不難發現基于 CAPM 的(de)殘差動量要比原始 UMD 更加顯著，這(zhè)背後的(de)原因恰恰就是上一自然段最後所指出的(de)。再來(lái)看控制了(le)因子動量後的(de)結果，無論是以常見因子構造因子動量，還(hái)是以主成分(fēn)因子構造動量，基于 CAPM、FF3 以及 FF5 的(de)殘差動量均不再顯著。而這(zhè)一結果在使用(yòng)主成分(fēn)因子構造因子動量時(shí)尤其精彩（三個(gè)版本的(de)殘差動量的(de) t-statistics 分(fēn)别爲 -0.38、0.04 以及 -0.03）。這(zhè)一結果的(de)含義是，盡管人(rén)們不知道 FF5 中到底遺漏了(le)哪些因子，但可(kě)以推斷這(zhè)些被遺漏因子和(hé)這(zhè) 10 個(gè)主成分(fēn)因子密切相關。

現在，讓我們來(lái)看實證的(de)最後一塊拼圖。

本文開篇曾提到 FF5 無法解釋動量（UMD）因子。事實上，任何一個(gè)不包含動量因子的(de) ad-hoc 簡約多(duō)因子模型似乎都很難解釋動量。這(zhè)背後的(de)原因是動量因子和(hé)其他(tā)因子在時(shí)序上的(de)非條件相關性很低。然而，這(zhè)一經驗事實低估了(le) UMD 和(hé)其他(tā)因子的(de)關系。

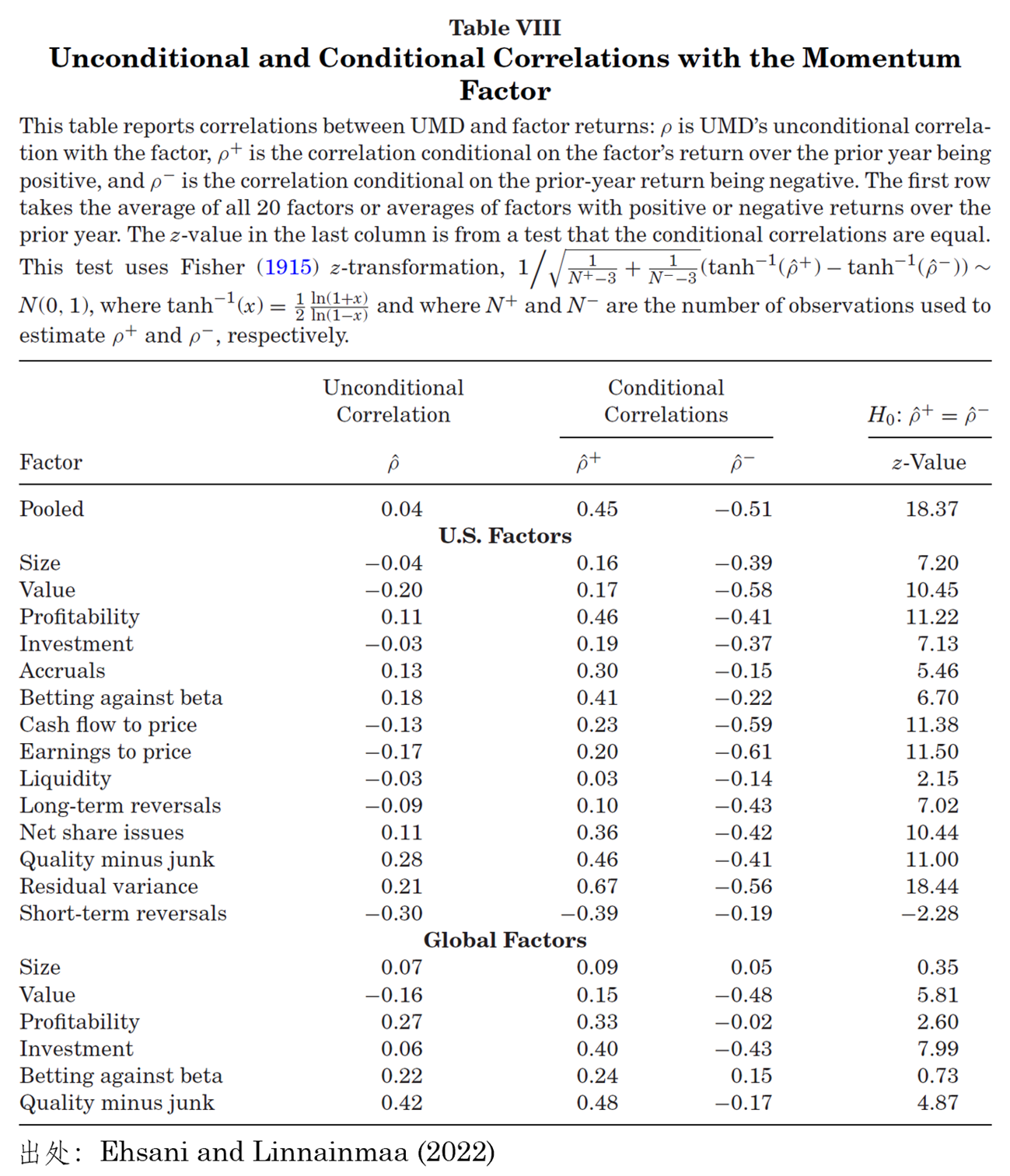
舉例來(lái)說，假如規模（Size）因子在過去表現很好，那麽人(rén)們在構造 UMD 因子時(shí)也(yě)會做(zuò)多(duō)小市值的(de)股票(piào)而做(zuò)空大(dà)市值的(de)股票(piào)。由于 Size 和(hé) UMD 都做(zuò)多(duō)小市值的(de)股票(piào)且做(zuò)空大(dà)市值的(de)股票(piào)，因此可(kě)以預期它們的(de)收益率在下(xià)一期是正相關的(de)。反之，如果 Size 表現很差，那麽 UMD 則會做(zuò)多(duō)大(dà)市值的(de)股票(piào)而做(zuò)空小市值的(de)股票(piào)，因此這(zhè)兩者下(xià)一期則很有可(kě)能負相關。同樣的(de)機制可(kě)以被用(yòng)于分(fēn)析 UMD 和(hé)其他(tā)别的(de)因子之間的(de)關系：當一個(gè)因子在過去一段時(shí)間表現很好，那麽它和(hé) UMD 在未來(lái)就更有可(kě)能正相關，反之則負相關。這(zhè)個(gè)分(fēn)析表明(míng)，如果以任意給定因子過去一段時(shí)間的(de)表現爲條件，來(lái)考察 UMD 和(hé)該因子的(de)條件相關性，那麽将會得(de)到不同的(de)答(dá)案。

下(xià)表給出了(le)實證結果。其中 $\rho$ 表示 UMD 和(hé)給定因子的(de)非條件相關系數； $\rho^+$ 表示當給定因子過去 12 個(gè)月(yuè)收益率爲正時(shí)，它和(hé) UMD 的(de)相關系數； $\rho^-$ 表示當給定因子過去 12 個(gè)月(yuè)收益率爲負時(shí)，它和(hé) UMD 的(de)相關系數。結果清晰的(de)展示出，雖然非條件相關性不高(gāo)，但一旦分(fēn)别考察 $\rho^+$ 和(hé) $\rho^-$ ，結果則完全不同。以美(měi)股因子爲例，除了(le)反轉外，其他(tā)所有因子的(de) $\rho^+$ 均大(dà)于零，而所有因子的(de) $\rho^-$ 均小于零。此外，兩位作者還(hái)對(duì) $\rho^+ = \rho^-$ 進行了(le)統計檢驗，對(duì)于所有因子而言，原假設均能被拒絕。

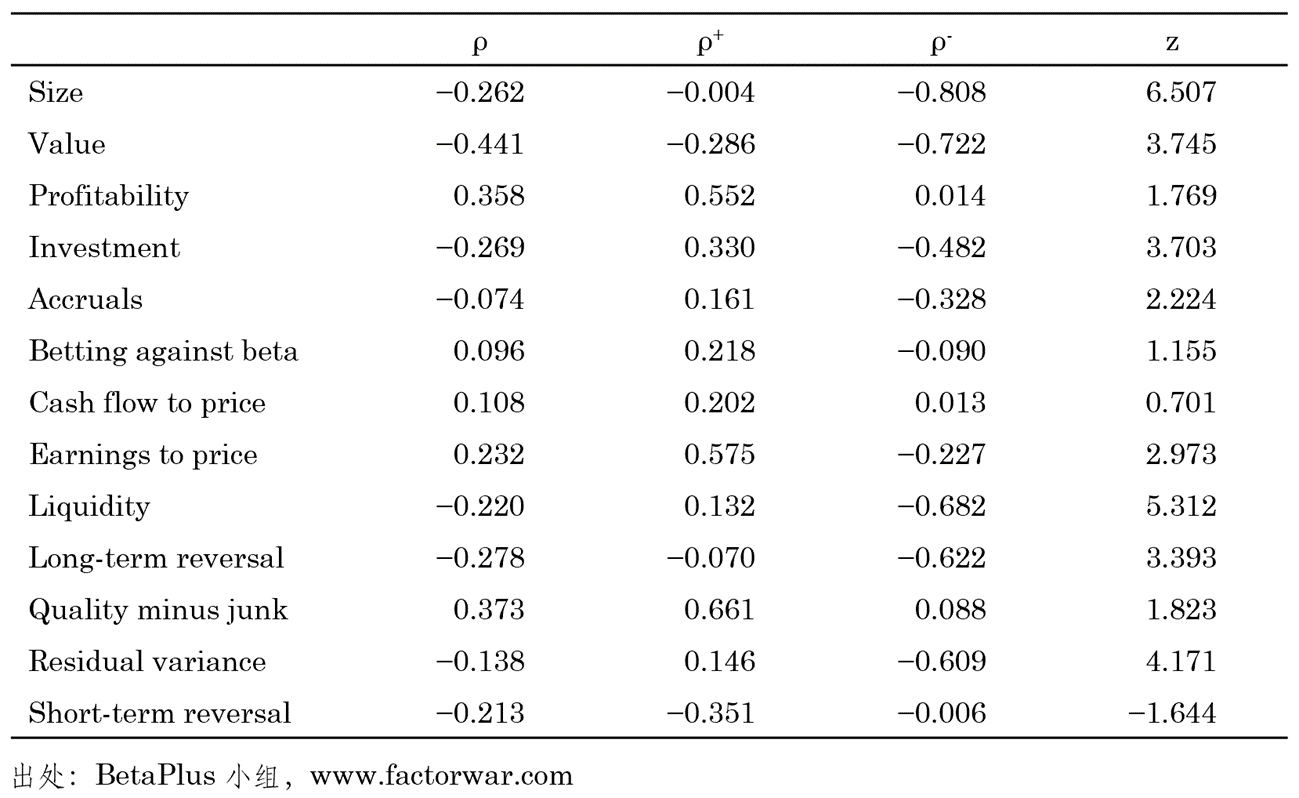
針對(duì) A 股的(de)實證結果如下(xià)。雖不如美(měi)股那麽明(míng)顯，但也(yě)在很大(dà)程度上是一緻的(de)。這(zhè)些結果均表明(míng)，UMD 因子和(hé)其他(tā)因子之間并非無關，而是它和(hé)其他(tā)因子時(shí)變的(de)條件相關性讓它顯得(de)和(hé)這(zhè)些因子非條件無關，從而也(yě)就造成了(le)非條件時(shí)序回歸時(shí)其他(tā)因子無法解釋它的(de)謎團。

以上就是我對(duì) Ehsani and Linnainmaa (2022) 的(de)解讀。雖然前面五個(gè)小節已經分(fēn)别回答(dá)了(le)本文一開始列出的(de)五個(gè)問題，但是在最後還(hái)是讓我再把它們放在一起總結一下(xià)：

問題一：因子收益率是否有時(shí)序自相關性？

回答(dá)一：絕大(dà)多(duō)數因子的(de)收益率存在自相關性。

問題二：因子滿足何種條件時(shí)，更容易出現自相關性？

回答(dá)二：和(hé)個(gè)股收益率協方差矩陣更相關的(de)因子，自相關性更強。

問題三：利用(yòng)自相關性、基于因子曆史收益率構造的(de)因子動量策略（注意，它類似于 UMD，是以因子組合爲 assets 的(de)截面動量策略）和(hé)個(gè)股截面動量因子（即 UMD）有什(shén)麽關系？誰是因？誰又是果？

回答(dá)三：因子動量能夠解釋個(gè)股動量（及其各種變化(huà)版本），但個(gè)股動量（及其各種版本）無法解釋因子動量。個(gè)股動量效應背後的(de)驅動（之一）是因子動量。

問題四：因子動量能否解釋個(gè)股殘差動量？

回答(dá)四：殘差動量是多(duō)因子模型中存在遺漏變量所緻，僅僅是被遺漏的(de)因子的(de)動量。一旦不存在模型設定偏誤，殘差動量消失。

問題五：如何理(lǐ)解 UMD 因子和(hé)其他(tā)因子時(shí)序無關的(de)實證現象？

回答(dá)五：當控制了(le)曆史收益率之後，UMD 因子和(hé)其他(tā)因子有很強的(de)正相關或負相關。UMD 因子和(hé)其他(tā)因子時(shí)變的(de)條件相關性使其看上去和(hé)其他(tā)因子非條件無關。

這(zhè)篇文章(zhāng)的(de)實證之細緻、結果之豐富、推論之重要，無一不令人(rén)拍(pāi)案叫絕。它無愧于 Journal of Finance，也(yě)值得(de)每一個(gè)研究和(hé)使用(yòng)動量的(de)小夥伴仔細品味，相信你一定會有收獲。Ehsani and Linnainmaa (2022) 于 2019 年 2 月(yuè)投稿，曆時(shí)兩年，2021 年3 月(yuè)被接收，2022 年最終見刊。然而，一切等待都值得(de)。

參考文獻

Asness, C. S., T. J. Moskowitz, and L. H. Pedersen (2013). Value and momentum everywhere. Journal of Finance 68(3), 929 – 985.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Ehsani, S. and J. T. Linnainmaa (2022). Factor momentum and the momentum factor. Journal of Finance 77(3), 1877 – 1919.

Fama, E. F. and K. R. French (2016). Dissecting anomalies with a five-factor model. Review of Financial Studies 29(1), 69 – 103.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

因子動量與動量因子