因子投資的(de)高(gāo)維數時(shí)代

作者：石川

摘要：實證資産定價已然進入因子（協變量）的(de)高(gāo)維數時(shí)代。本文抛磚引玉，闡述我對(duì)此的(de)四點思考。

0 引子

時(shí)至今日，實證資産定價（以及因子投資）已然步入了(le)因子（協變量）的(de)高(gāo)維數時(shí)代。大(dà)量發表在頂刊上的(de)實證結果表明(míng)，多(duō)因子模型具有很大(dà)的(de)不确定性且因子的(de)稀疏性假設不成立。人(rén)們熟知的(de) ad-hoc 簡約模型無法指引未來(lái)的(de)投資。在高(gāo)維數時(shí)代，尋找真正能夠預測預期收益率的(de)協變量是核心問題之一。爲了(le)實現這(zhè)個(gè)目标，需要考慮的(de)問題包括：（1）多(duō)重假設假設檢驗；（2）投資者（高(gāo)維）學習(xí)問題 & 另類數據；（3）來(lái)自資産定價理(lǐ)論的(de)指引：即解釋預期收益率的(de)因子應該也(yě)能解釋資産的(de)共同波動。最後，一個(gè)最新的(de)討(tǎo)論熱(rè)點是因子的(de)個(gè)數是否越多(duō)越好（即模型複雜(zá)度是否越高(gāo)越好）：複雜(zá)模型能更好地逼近真實 DGP，但參數估計的(de)方差更大(dà)；簡約模型的(de)參數估計更準确，但卻未必是 DGP 的(de)合理(lǐ)近似。二者相比，如何權衡呢(ne)？

近日，我在某券商 2023 的(de)年度策略會上做(zuò)了(le)題爲《因子投資的(de)高(gāo)維數時(shí)代》的(de)報告，闡述了(le)我對(duì)上述四點的(de)思考。本文借著(zhe)報告的(de) slides 做(zuò)簡要介紹。由于對(duì)于某些問題公衆号已經做(zuò)了(le)大(dà)量的(de)梳理(lǐ)（比如多(duō)重假設檢驗），因此在本文的(de)闡述中，在必要的(de)地方會使用(yòng)最少的(de)文字（你馬上就會明(míng)白我的(de)意思）。

1 多(duō)重假設檢驗

這(zhè)部分(fēn)，一圖勝千言。需要相關知識的(de)小夥伴，請查看公衆号的(de)《出色不如走運》系列。

Next.

2 投資者學習(xí)問題 & 另類數據

理(lǐ)性預期假設投資者知道真實的(de)估值模型。然而，和(hé)進行事後（ex post）因子分(fēn)析的(de)你我一樣，投資者在投資時(shí)同樣面臨協變量的(de)高(gāo)維數問題，因此不可(kě)能知道真實的(de)估值模型，所以理(lǐ)性預期假設并不成立。這(zhè)造成的(de)結果是，均衡狀态下(xià)資産價格和(hé)理(lǐ)性預期情況下(xià)相比出現偏差。在事後分(fēn)析中，已實現收益率中包含一部分(fēn)因估計誤差導緻的(de)可(kě)預測成分(fēn)。但對(duì)投資者來(lái)說，事前（ex ante）無法利用(yòng)上述可(kě)預測性。因誤差導緻的(de)可(kě)預測性能夠在樣本内（IS）産生虛假的(de)可(kě)預測性（無論投資者是否使用(yòng)了(le)先驗以及無論先驗是否正确），而在樣本外（OOS）卻無法預測收益率。這(zhè)就是投資者（高(gāo)維）學習(xí)問題導緻的(de)虛假的(de)可(kě)預測性（Martin and Nagel 2022）。具體闡述見《False In-Sample Predictability ?》。面對(duì)這(zhè)個(gè)問題，需要通(tōng)過 OOS 檢驗才能規避。

投資者無法在事前投資中應對(duì)高(gāo)維數，這(zhè)主要體現在他(tā)們使用(yòng)較少的(de)協變量（因子）作爲估值的(de)依據。另一方面，由于一些變量的(de)獲取成本很高(gāo)，投資者需要在該變量帶來(lái)的(de)預測好處和(hé)其成本之間權衡。此外，有限理(lǐ)性中的(de)有限注意力機制也(yě)爲投資者對(duì)簡約性的(de)渴望提供了(le)微觀基礎。這(zhè)兩方面作用(yòng)合力導緻投資者在爲資産定價時(shí)使用(yòng)過度稀疏的(de)估值模型。這(zhè)樣做(zuò)的(de)後果是，即便在樣本外，也(yě)會出現因投資者學習(xí)問題而造成的(de)虛假的(de)可(kě)預測性。

就著(zhe)上述推論，我們自然地引出本小節的(de)另一個(gè)相關話(huà)題：另類數據。回憶一下(xià)公衆号之前的(de)文章(zhāng)《科技關聯度II》所介紹的(de) Bekkerman, Fich and Khimich (forthcoming)。相比于之前的(de)基于專利類别的(de)研究，該文對(duì)專利進行文本分(fēn)析，通(tōng)過提取專業術語并計算(suàn)其重合度來(lái)描述公司之間的(de)相似程度，以此構造了(le)預期超額收益率更高(gāo)的(de)科技關聯度效應。比起專利類别，投資者在獲得(de)以及處理(lǐ)專利文本并計算(suàn)科技關聯度時(shí)的(de)成本更加昂貴。這(zhè)會導緻大(dà)多(duō)數投資者會在爲公司估值時(shí)忽略這(zhè)方面的(de)信息，即使用(yòng)過度稀疏的(de)估值模型，造成樣本内和(hé)樣本外收益率可(kě)預測性。該文基于文本分(fēn)析的(de)科技關聯度是近幾年大(dà)紅大(dà)紫的(de)基于另類數據進行實證資産定價和(hé)因子投資的(de)一個(gè)典型例子。然而，Martin and Nagel (2022) 所勾勒出的(de)非理(lǐ)性預期假設世界告訴我們，使用(yòng)最新的(de)方法和(hé)技術構建預測變量并将其應用(yòng)于早期曆史時(shí)段時(shí)，它們在樣本内和(hé)（僞）樣本外檢驗中均能預測預期收益率。因此，我們在驚喜于另類數據的(de)發現之餘，恐怕也(yě)應該多(duō)一分(fēn)謹慎。

除此之外，既然談到另類數據，不妨再聊聊另一個(gè)相關話(huà)題。有相關研究表明(míng)，海外大(dà)量的(de)另類數據供應商提供的(de)數據都隻具備對(duì)公司基本面的(de)短時(shí)間尺度的(de)可(kě)預測性。Dessaint, Foucault and Fresard (2020) 的(de)研究表明(míng)，如此另類數據可(kě)得(de)性的(de)提升降低了(le)進行短時(shí)間尺度的(de)預測成本（從而提高(gāo)了(le)準确性），但增加了(le)進行長(cháng)時(shí)間尺度預測的(de)成本（從而降低了(le)準确性）。對(duì)于公司基本面預測來(lái)說，二者的(de)綜合效果是 mixed。可(kě)以預見，未來(lái)在使用(yòng)另類數據預測公司基本面時(shí)，會有更多(duō)的(de)研究向這(zhè)個(gè)方向傾斜。

3 和(hé)協方差矩陣有關

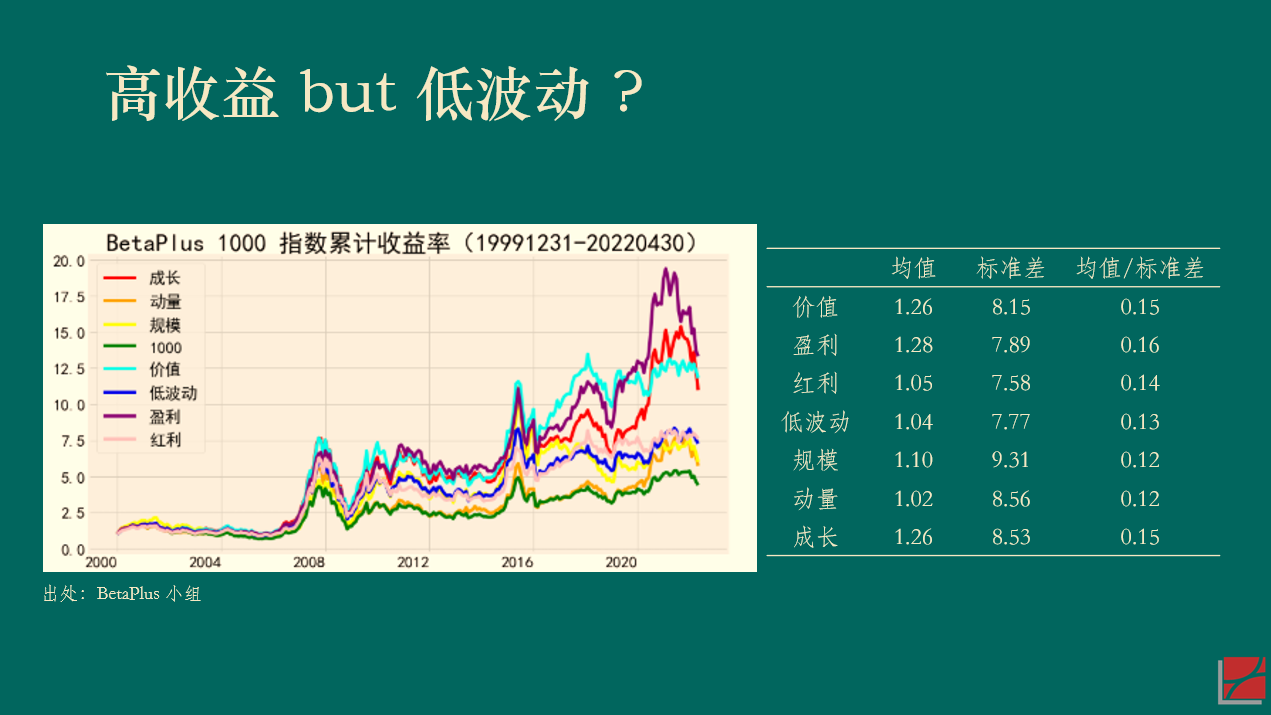
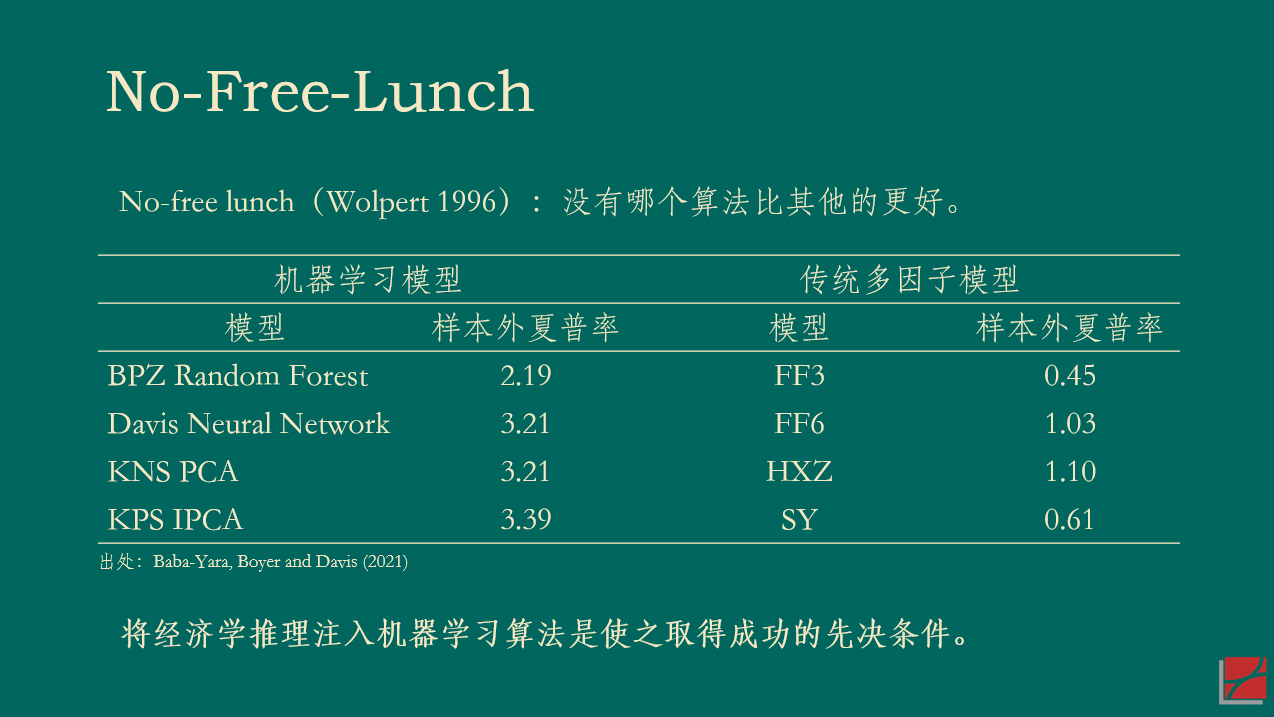
Ross (1976) 的(de) APT 指出，解釋資産預期收益率截面差異的(de)因子應該同時(shí)能夠解釋資産的(de)共同運動。在市場(chǎng)中不存在近似無風險套利機會這(zhè)個(gè)假設下(xià)，Kozak, Nagel and Santosh (2018) 同樣論述了(le)這(zhè)一點（見《Which beta (III)?》）。以下(xià)展示了(le) BetaPlus 小組構造并維護的(de) A 股常見七類風格因子在 2000/01/01 到 2022/04/30 之間的(de)表現。統計數據表明(míng)，在該實證區(qū)間内，雖然它們的(de)收益率均值高(gāo)低有差異，但收益率的(de)标準差同樣也(yě)有差異，因此并沒有哪個(gè)風格因子的(de)風險調整後收益明(míng)顯高(gāo)于其他(tā)的(de)因子。

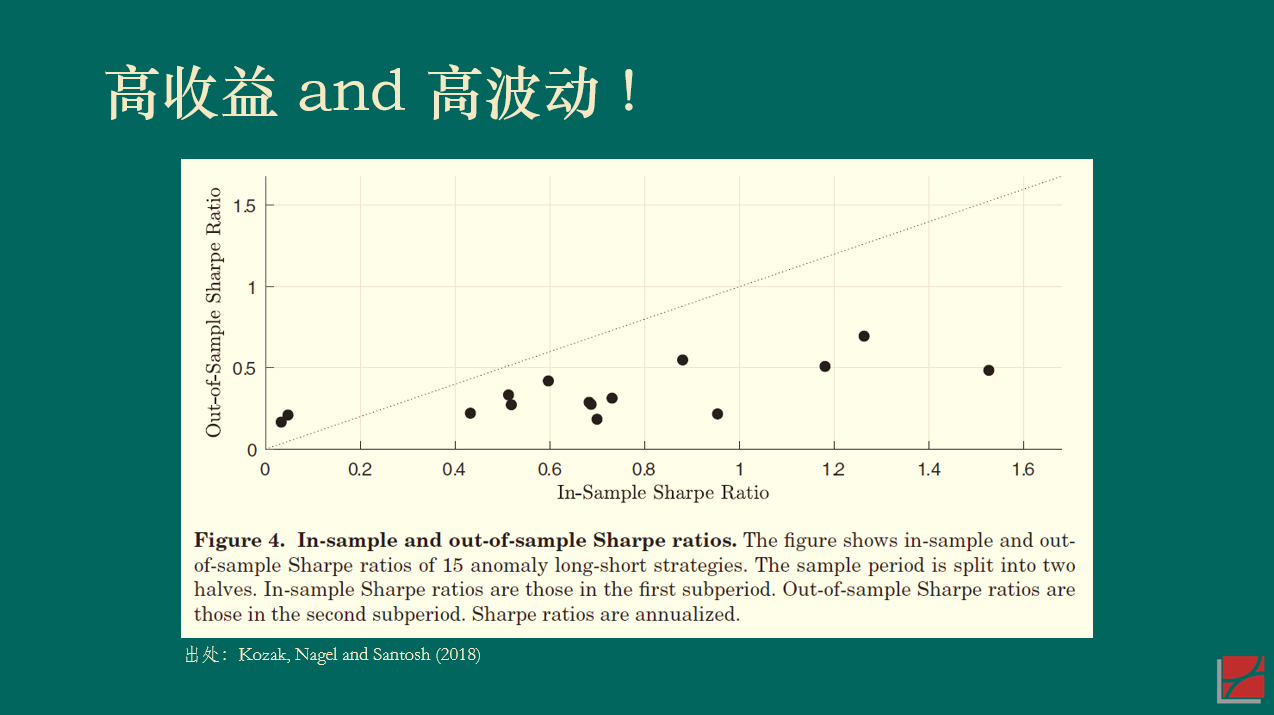
再來(lái)看一個(gè)美(měi)股的(de)例子。Kozak, Nagel and Santosh (2018) 将實證區(qū)間分(fēn)成前後兩半兒(ér)并考察了(le) 15 個(gè)因子。下(xià)圖展示了(le)每個(gè)因子在前後兩個(gè)區(qū)間内夏普率的(de)散點圖。如果能夠在獲得(de)高(gāo)收益的(de)同時(shí)降低波動，那麽樣本内（前一半區(qū)間）夏普率高(gāo)的(de)因子在樣本外（後一半區(qū)間）的(de)夏普率應該仍然更高(gāo)一些，我們将會看到這(zhè)些點圍繞在 45 度直線上。然而事實并非如此。無論樣本内的(de)夏普率多(duō)高(gāo)，這(zhè) 15 個(gè)因子樣本外的(de)夏普率幾乎是一條平行于橫坐(zuò)标的(de)水(shuǐ)平線，而非人(rén)們期望的(de) 45 度斜線。（我用(yòng)幾百個(gè)因子在 A 股做(zuò)了(le)同樣的(de)實證，觀察到了(le)類似的(de)結果。）

上述結果顯示，（樣本外）高(gāo)收益往往對(duì)應著(zhe)高(gāo)波動（對(duì)著(zhe)樣本内硬挖 —— data snooping —— 另說），這(zhè)一實證結果和(hé) APT 吻合。早在幾十年前，Eugene Fama 曾經打趣到 APT 讓衆多(duō)挖因子的(de)嘗試“合理(lǐ)化(huà)”，即 APT 隻說了(le)資産預期收益率和(hé)衆多(duō)因子有關，但卻沒有指出到底有哪些因子。因此，很多(duō)學者打著(zhe) APT 的(de)旗号“肆無忌憚”地挖出了(le)一茬又一茬因子（zoo of factors），Fama 把這(zhè)個(gè)現象稱作 APT 給了(le)這(zhè)些研究“fishing license”（即 APT 讓這(zhè)些研究合理(lǐ)化(huà)）。（Sorry，這(zhè)裏我實在忍不住吐槽一句，在一本著名的(de)資産定價教材的(de)中譯版中，中文作者竟然真的(de)把 fishing license 翻譯成“釣魚許可(kě)證”……）如今，當我們重新審視 APT 時(shí)，毫無疑問應該将它作爲挖掘真實因子的(de)有效指引，正如本節一開頭說的(de)那樣：解釋資産預期收益率截面差異的(de)因子應該也(yě)能解釋資産的(de)共同運動。在這(zhè)個(gè)認知下(xià)，以 PCA 爲代表的(de)一系列實證資産定價研究在這(zhè)幾年取得(de)了(le)很多(duō)突破（Kelly, Pruitt and Su 2019 、Kozak, Nagel and Santosh 2020）。

4 越複雜(zá)越好 ?

在本節的(de)討(tǎo)論中，我們以因子個(gè)數的(de)多(duō)少代表模型複雜(zá)度。因子個(gè)數越多(duō)，模型越複雜(zá)。

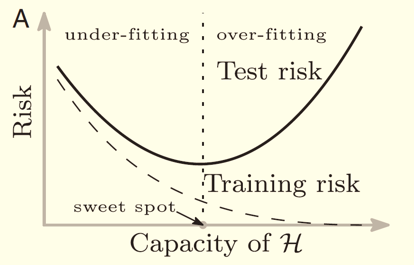
2019 年，Belkin, et al. (2019) 一文提出了(le)機器學習(xí)中樣本外誤差的(de)“double descent”現象，引發了(le)機器學習(xí)領域和(hé)理(lǐ)論統計領域的(de)廣泛討(tǎo)論。爲了(le)理(lǐ)解這(zhè)一現象，我們先從熟知的(de) bias-variance trade-off 說起。對(duì)于模型來(lái)說，其樣本外表現和(hé)模型複雜(zá)度關系密切。當模型複雜(zá)度很低時(shí)，模型的(de)方差很小（因爲變量參數估計的(de)方差很小），但是偏差很高(gāo)；當模型複雜(zá)度高(gāo)時(shí)，模型的(de)方差變大(dà)，但是偏差降低。二者的(de)共同作用(yòng)就是人(rén)們熟悉的(de) U-Shape，即 bias-variance trade-off，因此存在某個(gè)最優的(de)超參數，使得(de)樣本外的(de)總誤差（風險）最低。

我們還(hái)可(kě)以換個(gè)角度來(lái)理(lǐ)解 bias-variance trade-off，而這(zhè)個(gè)角度對(duì)理(lǐ)解 double descent 至關重要。當模型很簡單時(shí)，它能夠有效規避過拟合，但卻很難想象如此簡單的(de)模型是真實世界的(de)好的(de)近似；而當模型複雜(zá)時(shí)，它更有可(kě)能逼近真實世界，但是也(yě)的(de)确更容易過拟合。因此 bias-variance trade-off 也(yě)可(kě)以理(lǐ)解爲 approximation-overfit trade-off。然而，上述結論有一個(gè)我們都習(xí)以爲常的(de)前提：變量個(gè)數 < 樣本個(gè)數。那麽，如果模型複雜(zá)到變量（因子）的(de)個(gè)數超過了(le)樣本的(de)個(gè)數又會出現怎樣的(de)情況呢(ne)？事實上，這(zhè)一問題并非無緣無故的(de)憑空想象。對(duì)于複雜(zá)的(de)神經網絡模型來(lái)說，模型參數的(de)個(gè)數很容易超過樣本的(de)個(gè)數，然而這(zhè)些模型确在樣本外有著(zhe)非凡的(de)表現（哦，當然不是資産定價領域）。這(zhè)個(gè)現象促使這(zhè)人(rén)們搞清楚 what is behind the scene。

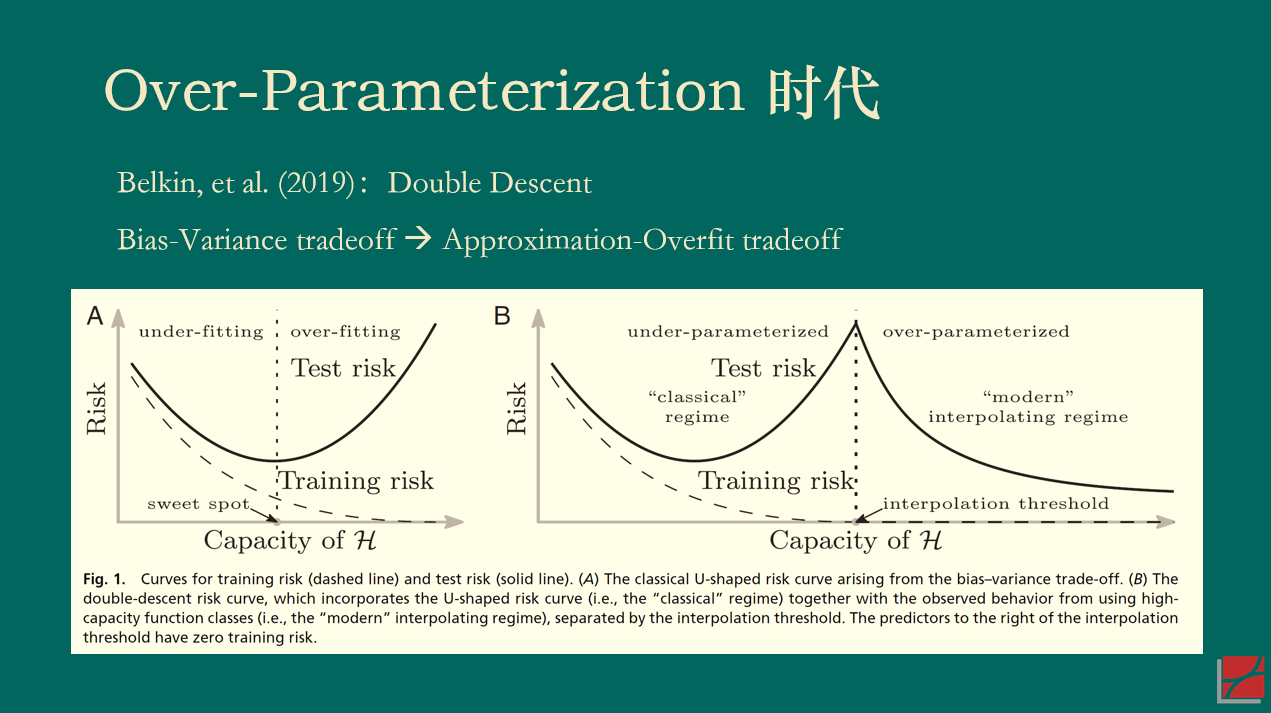
當變量個(gè)數 > 樣本個(gè)數時(shí)，模型在樣本内能夠完美(měi)的(de)拟合全部樣本（在機器學習(xí)術語中，這(zhè)個(gè)現象被稱爲 interpolation）。對(duì)這(zhè)樣一個(gè)模型來(lái)說，人(rén)們通(tōng)常的(de)認知是，它在樣本外的(de)表現一定會“爆炸”，即毫無作爲。這(zhè)是因爲它過度拟合了(le)樣本内數據中的(de)全部噪聲。然而，Belkin, et al (2019) 指出，當人(rén)們讓模型複雜(zá)度突破樣本個(gè)數這(zhè)個(gè)“禁忌之地”後，神奇的(de)事情發生了(le)：樣本外總誤差并沒有“爆炸”，而是随著(zhe)複雜(zá)度的(de)提升單調下(xià)降。正因爲在樣本個(gè)數兩側都出現了(le)誤差單調下(xià)降的(de)情況，Belkin, et al (2019) 将這(zhè)個(gè)現象稱爲 double descent。

因爲本文的(de)目的(de)并非解釋背後的(de)統計學理(lǐ)論，所以我在此對(duì)該現象給一些直覺上的(de)解釋。當變量個(gè)數超過樣本個(gè)數的(de)時(shí)候，樣本内的(de)解是不唯一的(de)，而最優的(de)解可(kě)以理(lǐ)解爲滿足參數的(de)方差最小（正則化(huà)或 implied 正則化(huà)在這(zhè)個(gè)過程中發揮了(le)非常重要的(de)作用(yòng)）。随著(zhe)變量越來(lái)越多(duō)，最優解的(de)方差總能單調下(xià)降。再來(lái)看偏差，通(tōng)常來(lái)說，偏差确實會随著(zhe)複雜(zá)度的(de)提升而增加。但是所有模型都是真實 DGP 的(de)某個(gè) mis-specified 版本。當存在模型設定偏誤的(de)時(shí)候，可(kě)以證明(míng)當變量個(gè)數超過樣本個(gè)數時(shí)，偏差也(yě)會在一定範圍内随著(zhe)複雜(zá)度而下(xià)降。因此，二者的(de)綜合結果就是模型在樣本外的(de)誤差表現會随複雜(zá)度的(de)上升而下(xià)降。（在一些情況下(xià)，樣本外誤差的(de) global minimum 出現在當變量個(gè)數 > 樣本個(gè)數時(shí)。）以下(xià)兩張 slides 總結了(le)上面的(de)話(huà)（第二張 slide 裏的(de)表參考了(le) Bryan Kelly 的(de) talk，特此說明(míng)）。

對(duì)于資産定價和(hé)因子投資來(lái)說，如果你和(hé)我一樣認同因子的(de)高(gāo)維數時(shí)代 —— 即收益率的(de) DGP 包含了(le)非常多(duō)的(de)因子，那麽上述關于模型複雜(zá)度的(de)探討(tǎo)也(yě)許會帶來(lái)全新而有益的(de)啓發。在這(zhè)方面，也(yě)有大(dà)佬已經走在了(le)前面。Bryan Kelly 和(hé)他(tā)的(de)合作者以及學生一起寫了(le)一系列“複雜(zá)度美(měi)德”的(de) working papers，在資産定價領域探索提升複雜(zá)度帶來(lái)的(de)樣本外好處。例如，Kelly, Malamud and Zhou (2022) 一文使用(yòng)神經網絡對(duì)美(měi)股進行了(le)擇時(shí)（每次建模僅利用(yòng)一年 12 期的(de)數據訓練神經網絡），并發現了(le)類似的(de) double descent 現象。當然，即便我們認同了(le)“越複雜(zá)越好”，也(yě)依然要回答(dá)更重要的(de)問題，即如何估計參數，如何正則化(huà)，如何來(lái)利用(yòng)成千上萬甚至更多(duō)的(de)因子來(lái)形成關于預期收益率更好的(de)預測。雖然 Kelly 等人(rén)的(de)文章(zhāng)在擇時(shí)方面取得(de)了(le)讓人(rén)興奮的(de)結果，但在 cross-section 是否有類似的(de)實證結果依然需要時(shí)間來(lái)回答(dá)（Kelly 有一篇 working paper 研究 cross-section，但還(hái)沒有 publicly available）。但是無論如何，歡迎來(lái)到 over-parameterization 時(shí)代。

5 結束語

在本文的(de)最後，仍然有必要指出，在協變量的(de)高(gāo)維數時(shí)代，如何 prepare 因子固然重要（小心多(duō)重假設檢驗、小心投資者學習(xí)、利用(yòng) APT 的(de) implication），但是如何求解高(gāo)維問題才更加核心（如何利用(yòng)複雜(zá)度的(de)好處 ?）。或許，我們已經到了(le)從計量經濟學到機器學習(xí)的(de)必然轉型時(shí)刻。正如 Stefan Nagel 的(de)《機器學習(xí)與資産定價》（Nagel 2021）所倡導的(de)那樣，将經濟學推理(lǐ)注入機器學習(xí)算(suàn)法将成爲高(gāo)維數時(shí)代研究的(de)必經之路。

參考文獻

Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.

Bekkerman, R., E. M. Fich, and N. V. Khimich (forthcoming). The effect of innovation similarity on asset prices: Evidence from patents’ big data. Review of Asset Pricing Studies.

Belkin, M., D. Hsu, S. Ma, and S. Mandal (2019). Reconciling modern machine-learning practice and the classical bias-variance trade-off. PNAS 116(32), 15849 – 15854.

Dessaint, O., T. Foucault, and L. Fresard (2020). Does alternative data improve financial forecasting? The horizon effect. Working paper.

Kelly, B. T., S. Malamud, and K. Zhou (2022). The virtue of complexity in return prediction. Working paper.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Linnainmaa, J. T. and M. R. Roberts (2018). The history of the cross-section of stock returns. Review of Financial Studies 31(7), 2606 – 2649.

Martin, I. and S. Nagel (2022). Market efficiency in the age of big data. Journal of Financial Economics 145(1), 154 – 177.

Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。